
九九の一の段は覚えなくてもいい
前回「九九は両手の中に!?」では、両手で九九を計算する方法を使えば、81個のうち25個(図の赤部分)を覚える必要がなくなり56個(図の橙部分)を覚えればよいことを紹介しました。
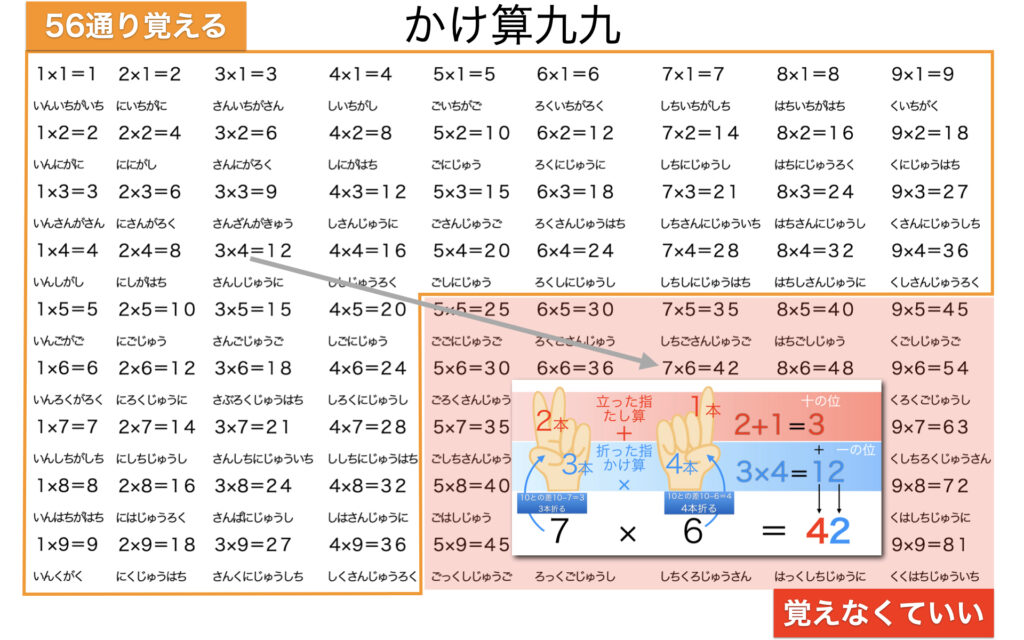
覚える必要がないものを考えていくと、一の段および□×1=□が思い浮かびます。
1×1=1(いんいちがいち)
1×2=2(いんにがに)、2×1=2(にいちがに)
1×3=3(いんさんがさん)、3×1=3(さんいちがさん)
1×4=4(いんしがし)、4×1=4(しいちがし)
1×5=5(いんごがご)、5×1=5(ごいちがご)
1×6=6(いんろくがろく)、6×1=6(ろくいちがろく)
1×7=7(いんしちがしち)、7×1=7(しちいちがしち)
1×8=8(いんはちがはち)、8×1=8(はちいちがはち)
1×9=9(いんくがく)、9×1=9(くいちがく)
以上17個。
さらに、9×8=72(くはしちじゅうに)はわすれても、8×9=72(はっくしちじゅうに)を思い出せば大丈夫。。すなわち、(大きい数)×(小さい数)も覚えなくても大丈夫。
3×2=6(さんにがろく)
4×2=8(しにがはち)、4×3=12(しさんじゅうに)
5×2=10(ごにじゅう)、5×3=15(ごさんじゅうご)、5×4=20(ごしにじゅう)
6×2=12(ろくにじゅうに)、6×3=18(ろくさんじゅうはち)、6×4=24(ろくしにじゅうし)、6×5=30(ろくごさんじゅう)
7×2=14(しちにじゅうし)、7×3=21(しちさんにじゅういち)、7×4=28(しちしにじゅうはち)、7×5=35(しちごさんじゅうご)、7×6=42(しちろくしじゅうに)
8×2=16(はちにじゅうろく)、8×3=24(はちさんにじゅうし)、8×4=32(はちしさんじゅうに)、8×5=40(はちごしじゅう)、8×6=48(はちろくしじゅうはち)、8×7=56(はちしちごじゅうろく)
9×2=18(くにじゅうはち)、9×3=27(くさんにじゅうしち)、9×4=36(くしさんじゅうろく)、9×5=45(くごしじゅうご)、9×6=54(くろくごじゅうし)、9×7=63(くしちろくじゅうさん)、9×8=72(くはちしちじゅうに)
以上1+2+3+4+5+6+7=28個。
こうして合計17+28=45個を覚えなくても大丈夫だと分かります。結局81−45=36個を覚えれば済むことになります。
81個の九九の半分以上の45個は覚えなくてもいいということです。こんなことならはじめから必要な36個だけ覚えればよいことを教科書にのせてくれればいいのにとおもいませんか。

江戸時代の教科書の九九は36個!?
そんな教科書が江戸時代にありました。『塵劫記』です。吉田光由によって1627年につくられた数学の教科書です。当時一家に一冊あっといわれるほどの江戸時代の大ベストセラーでした。 寺子屋の教科書として普及し、庶民が数学に興味を持つきっかけをつくった数学書です。この『塵劫記』に紹介されている九九は36通りだけ。

見事に一の段(□×1=□)と(大きい数)×(小さい数)の九九が省かれているのがわかります。
次の塵劫記では一の段は残されて、先ほどと同様に(大きい数)×(小さい数)の九九は省かれています。a×bは「abの」と発声することが記載されています。 四の段からは「の」がなくなっています。

江戸時代はわり算の九九もあった!?
塵劫記はそろばんのマニュアル書としても重宝されました。その中にわり算の九九がそろばんの珠の動かし方とともに説明されます。割り声(わりごえ)、割り声(わりせい)とも呼ばれます。
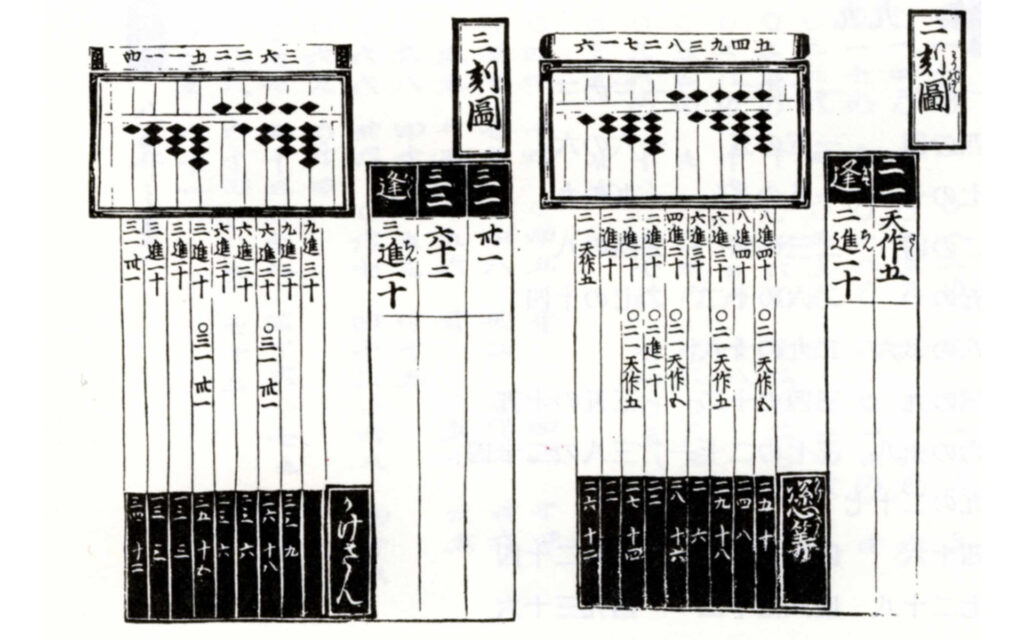
右ページが2で割る割算九九。
「二一天作五(にいちてんさくのご)」は、 「10を2で割れば商が5」のことで、そろばんでは十の位の一の珠をはらい、桁の上の珠を1つ降ろして五とおくことを表します。「(逢)二進一十(にっちんがいっしん)」は、「20を2で割れば商が10」のこと。
左ページは3で割る割算九九。
「三一三十一(さんいちさんじゅうのいち)」は、「10を3で割れば商が 3で余りが1」のこと。「三二六十二(さんにろくじゅうのに)」は、「20を3で割れば商が6で余りが2」のこと。「(逢)三進一十(さんちんがいっしん)」は、「30を3で割れば商が10」のこと。
「にっちもさっちもいかない」の語源はわり算九九!?
行き詰まってどうにも動きが取れない様子を表す時に用いられるのが「にっちもさっちもいかない」。漢字で書くと「二進も三進も行かない」。いま説明した「二進(にっちん)」「三進(さんちん)」です。
そろばんで2でも3でも割れない場合、そろばんの玉が動かせなくなります。これを「にっちんさんちんいかない」と言いました。これから「にっちもさっちもいかない」が生まれました。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






