7の倍数判定法は特別
2の倍数判定法は一の位が2の倍数、3の倍数判定法は桁の和が3の倍数、4の倍数判定法は十の位以下が4の倍数、5の倍数判定法は一の位が0か5、6の倍数判定法は一の位が2の倍数で桁の和が3の倍数、9の倍数判定法は桁の和が9の倍数、10の倍数判定法は一の位が0。
7と8の倍数判定法はこうは簡単にいきません。筆者が考案した7の倍数判定法を紹介しましょう。
84、91、98の3つを覚える
2桁の数の場合は、14、21、28、35、42、49、56、63は九九の7の段。次の70、77は7の倍数であることはすぐに分かります。残り84、91、98の3つを覚えておきます。
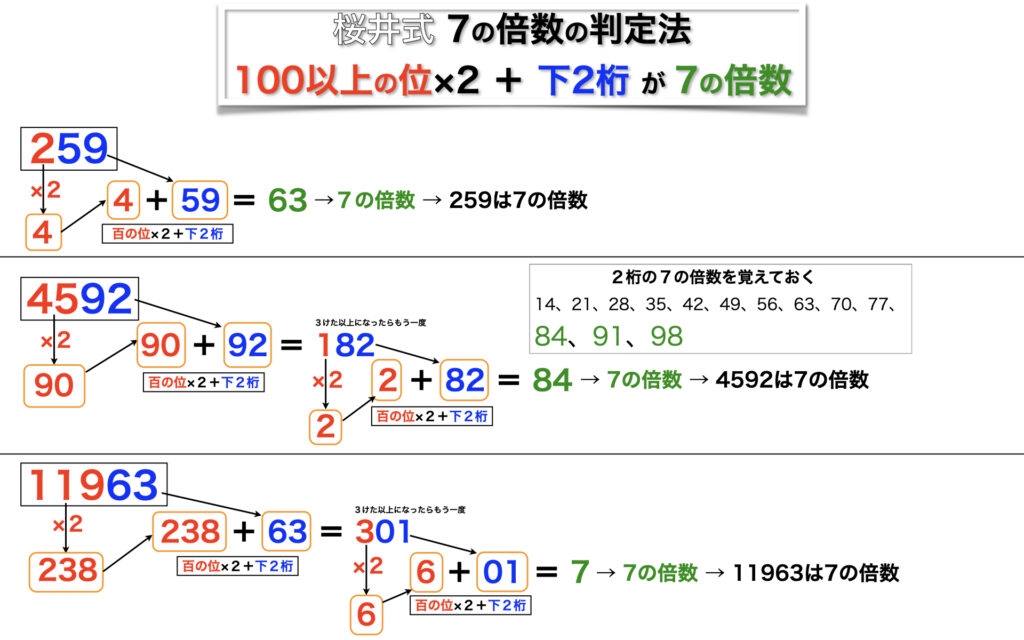
3桁以上の数の場合は、「百以上の位×2+下2桁が7の倍数」が7の倍数判定法。259を例に説明してみます。259を百以上の位2と下2桁59に分けます。百以上の位×2+下2桁を計算します。2×2+59=4+59=63、これは7の倍数なので259も7の倍数と判定できます。
桜井式7の倍数判定法「百以上の位×2+下2桁が7の倍数」
4592なら、45と92に分けます。45×2+92=182。これが3桁以上の場合には、この数に対して7の倍数判定法を適用します。1と82に分けて、1×2+82=84。これは7の倍数なので4592も7の倍数と判定できます。
11963なら、119と63に分けます、119×2+63=301。3桁なので同じ計算を繰り返します。3と01に分けて、3×2+01=7。これは7の倍数なので11963も7の倍数と判定できます。
6桁以上の場合
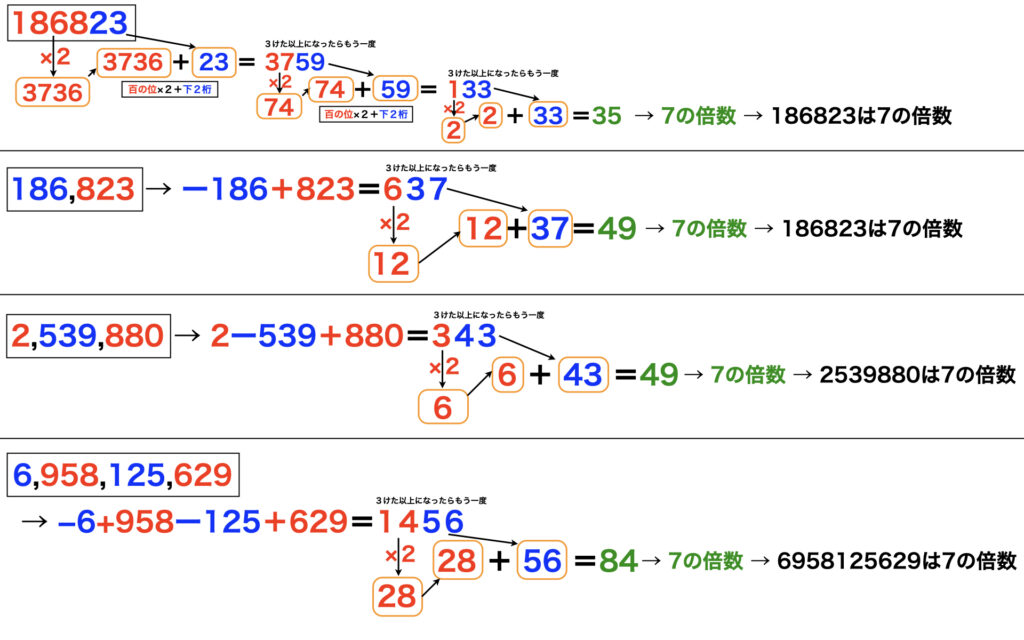
6桁186823ではどうでしょう。これまで同様1868と23に分けて「百以上の位×2+下2桁」でも計算できます。3759→133→35となり7の倍数であることが分かります。
6桁以上の場合には、一の位から3桁ずつに分けて、右から+、−、+、−、…の順に符号をつけて和を計算。こうすることで桁数を小さくすることができます。その後に「百以上の位×2+下2桁」を計算します。
186823を186と823に分けます。右から+または−の符合を交互につけて和を求めます。−186+823=637。「百以上の位×2+下2桁」の計算をします。6と37に分けて、6×2+37=49。これは7の倍数なので186823も7の倍数。
6958125629なら、6,958,125,629とカンマをつけて3桁ずつに分けます。右から+、−を交互につけて合計します。−6+958−125+629=1456。「百以上の位×2+下2桁」の計算をします。14と56に分けて、14×2+56=84。これは7の倍数なので6958125629も7の倍数。実際に7で割ってみれば、6958125629÷7=994017947。たしかに7の倍数です。
このように、7の倍数の判定はお世辞にも簡単だとはいえません。実際に使うというよりも、桜井式7の倍数判定法の計算を通して数の世界には法則があることを自分の目で確かめてみましょう。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





