
イタリアの数学者フィボナッチ
フィボナッチ数で知られるフィボナッチとはイタリアの数学者レオナルド・フィボナッチ(1170頃-1250頃)が由来です。1202年に『算盤の書』を著しました。その中でアラビア数字を次のように「インドの方法」として紹介しています。
このような数の表し方(位取り記数法)を用いた簿記、単位の変換、利子の計算などを説明しています。はたして、ヨーロッパの人々に大きな影響を及ぼすことになりました。

フィボナッチによるウサギの問題
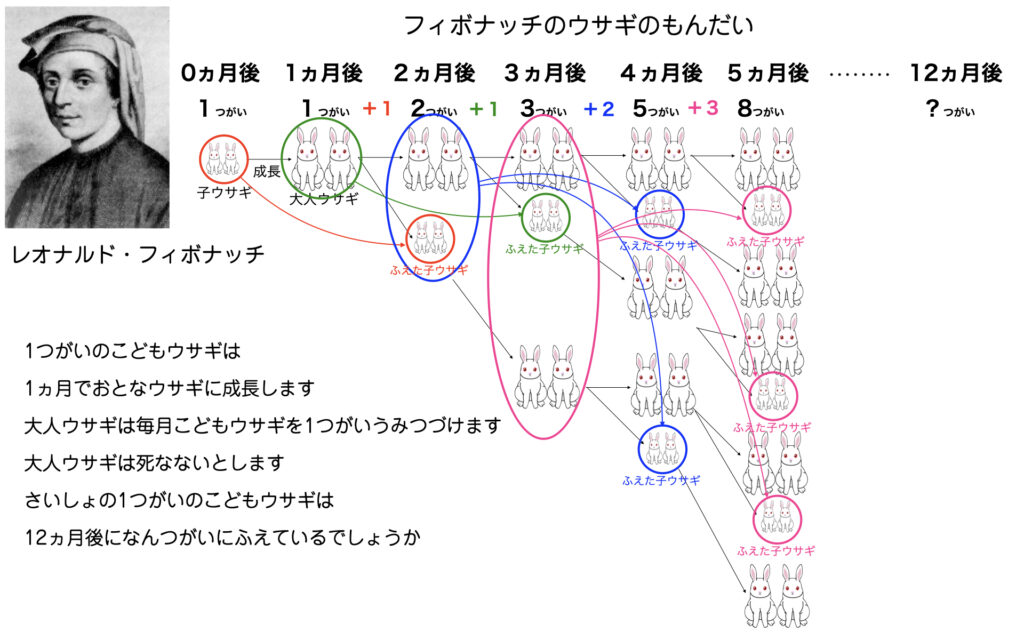
『算盤の書』ではまた、ウサギの増え方の問題が紹介されています。
2ヶ月後、大人ウサギとなり1つがいの子ウサギを産み、合計1+1=2つがい。
3ヶ月後、最初の1つがいのウサギは1つがいの子ウサギを産み続けるので合計2+1=3つがい。
4ヶ月後、最初の1つがいウサギの他に2ヶ月後に産まれた1つがいの子ウサギも大人ウサギになり1つがいの子ウサギを産みはじめるので、合計は3+2=5つがい。
では、5ヶ月後の合計はいくつだろうか?
フィボナッチの解説
次々と追っていくとウサギのつがいの増え方のルールがわかっていく。4ヶ月後のつがいの合計は3か月後のつがいの合計に2ヶ月後のつがいの合計を加えた値だとわかる。すると、ある月のつがいの合計は、その1ヶ月前のそれに2ヶ月前のそれを加えた値に等しいということ。したがって、この計算ルールを12ヶ月後まで続けていけば答えが求まる。
0ヶ月後1
1ヶ月後1
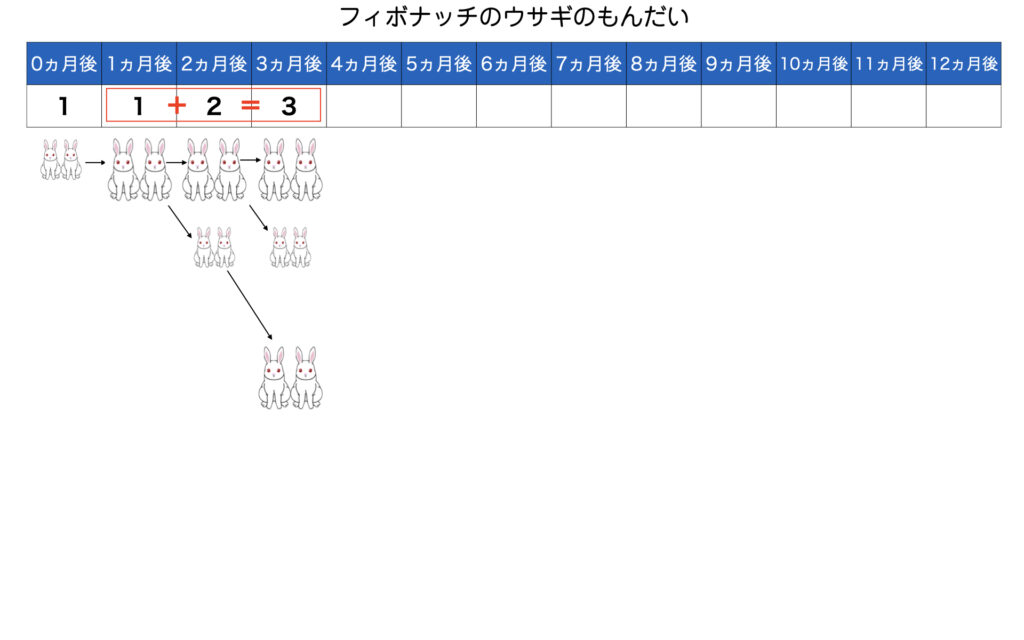
2ヶ月後1+1=2
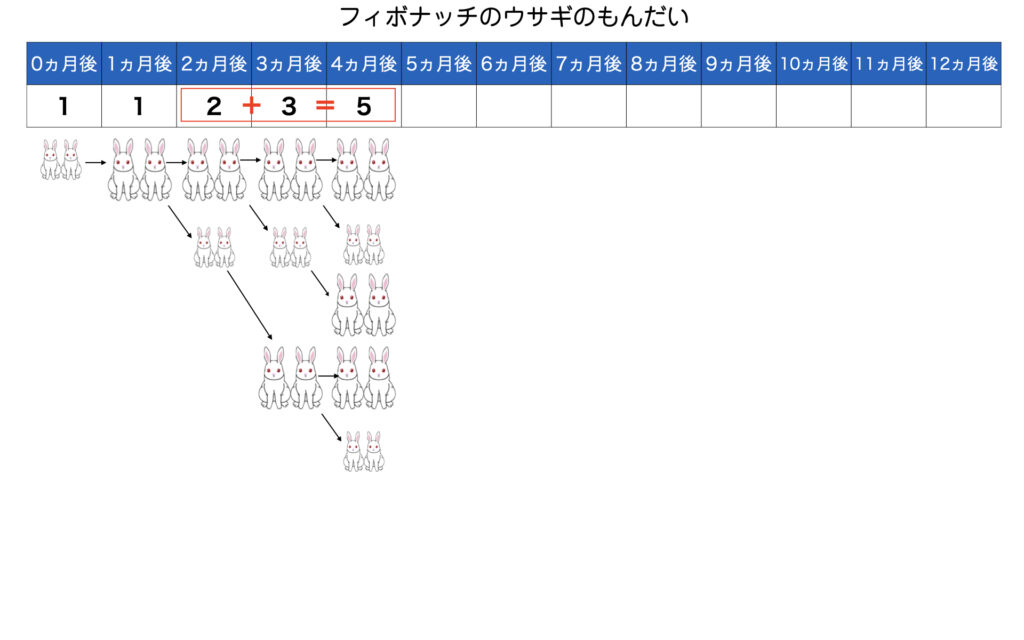
3ヶ月後2+1=3
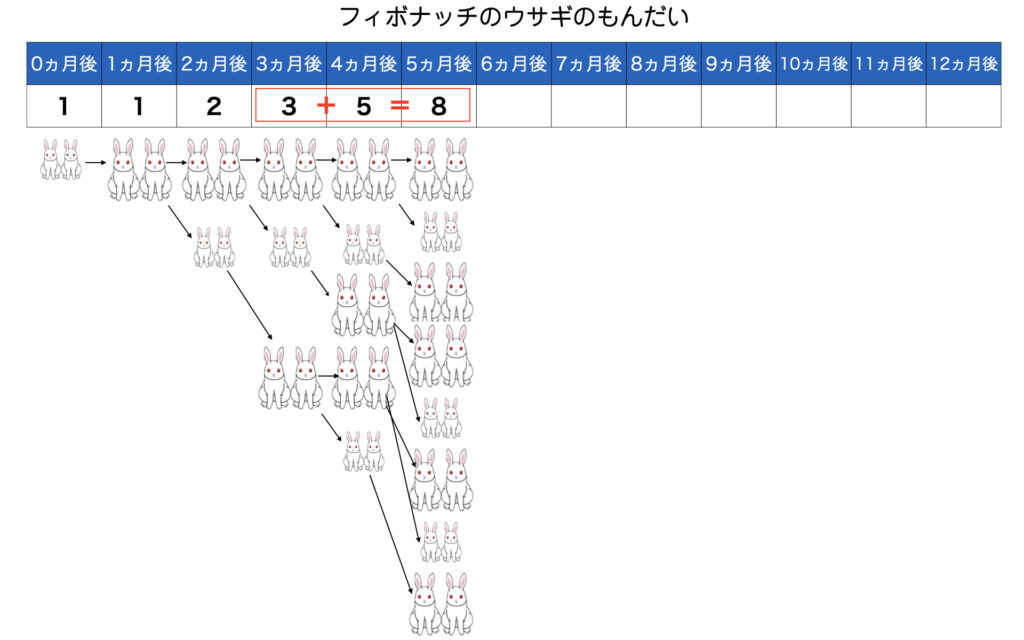
4ヶ月後3+2=5
5ヶ月後5+3=8
6ヶ月後8+5=13
7ヶ月後13+8=21
8ヶ月後21+13=34
9ヶ月後34+21=55
10ヶ月後55+34=89
11ヶ月後89+55=144
12ヶ月後144+89=233となり答えは233つがい。


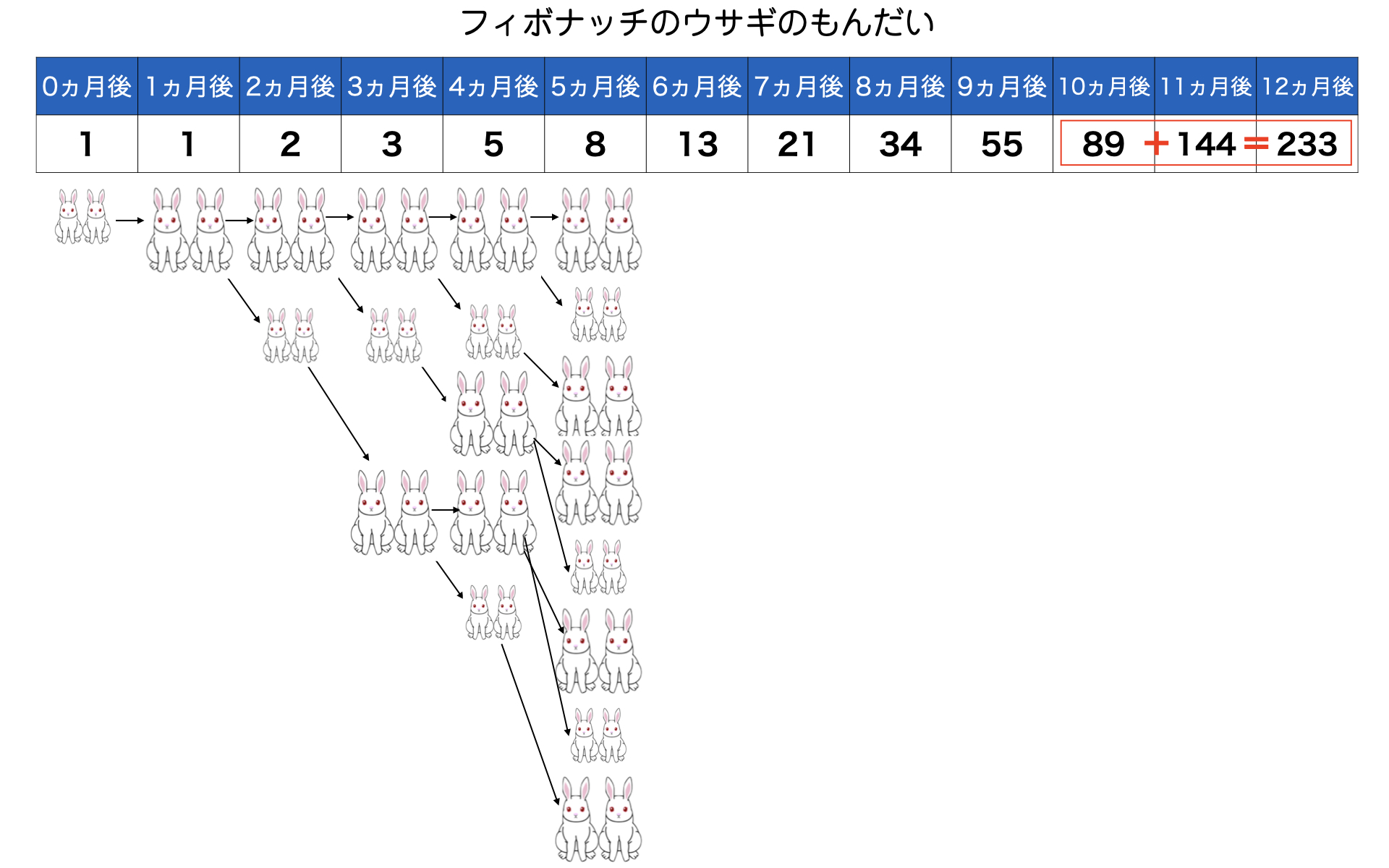
この解答に登場した1、1、2、3、5、8、…という数(まとめて数列と呼ぶ)が後にフィボナッチ数、フィボナッチ数列として知られるようになりました。この数もアラビア数字同様にインドでは知られていましたが、ヨーロッパに初めて紹介したのがフィボナッチです。
フィボナッチ数とフィボナッチ数列
フィボナッチ数は1、1、2、3、5、8、…のようにたくさんあります。これを数学では数列と呼びます。n番目フィボナッチ数をFnのように表すのが数列で、この添字のnは数列のn番目を表し、n番目の項を第n頂と呼びます。F₁₀=55はフィボナッチ数列の第10項が55であることを表します。また、数列の始まりの項を初項と呼びます。フィボナッチ数列の初項は2つF₁=1とF₂=1です。
フィボナッチ数をフィボナッチ数列としてとらえることで、フィボナッチ数の間の関係(ルール)をF₃=F₁+F₂、F₄=F₂+F₃、F₅=F₃+F₄のように明瞭に表すことができるようになります。

樹木の枝振り
次の図は1つの樹木の枝の生え方の説明です。1つの芽から1本の枝が生えるところから始まります。その枝が生長すると次の段階で枝分かれして新しい枝が生えます(図の左側の「新しい枝」)。
図の右側の「元の枝」は次の成長段階で枝分かれを続けていきます。「新しい枝」は次の成長はそのまま大きくなり、そして次の成長段階で枝分かれします。それが図の「新しい枝が枝分かれ」部分。
成長を段階ごとに下から上に枝の本数を数えていくと
1本→1本→2本→3本→5本→8本→13本→…
となりフィボナッチ数となることがわかります。
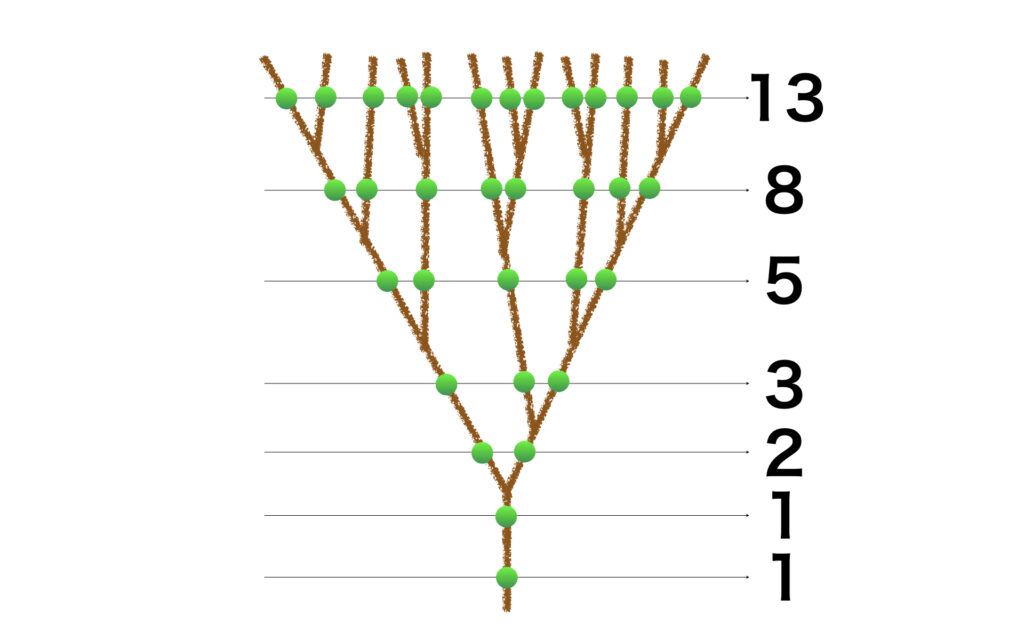
ウサギのつがいの増え方と樹木の枝分かれの仕方とが同じように考えることができるところが興味深いです。次回「フィボナッチ数の不思議 応用編」では、フィボナッチ数のさらなる不思議に迫っていきます。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






