よく目にする「味の黄金比率」「調味料の黄金比率」
調味料は何種類かを混ぜることで新しい味をつくることができます。そこで問題になるのが数種類の調味料を混ぜる割合です。いくつか紹介してみましょう。
どんな料理にもあうのが有名なオーロラソース。日本では、マヨネース:トマトケチャップ=1:1。和風煮物ではしょうゆ:砂糖:みりん=1:1:1。チキン南蛮にあう甘酢だれは、しょうゆ:砂糖:酢=1:1:1。味噌味の豚肉と野菜の炒め物では、味噌:砂糖:酒=1:1:1。
これらは、これで味が決まる「1:1:1の黄金比率」などと呼ばれています。味付けは甘すぎても、しょっぱすぎても美味しくありません。味にとって大切なのは割合・バランスだということです。絶妙な味付けの調合比率が味の黄金比率と呼ばれています。
どの長方形が好み?
もともとの黄金比は数学の中で発見されました。二千年以上も昔、いかにして古代ギリシャの数学者は絶妙な比率を発見したのでしょうか。探っていきます。
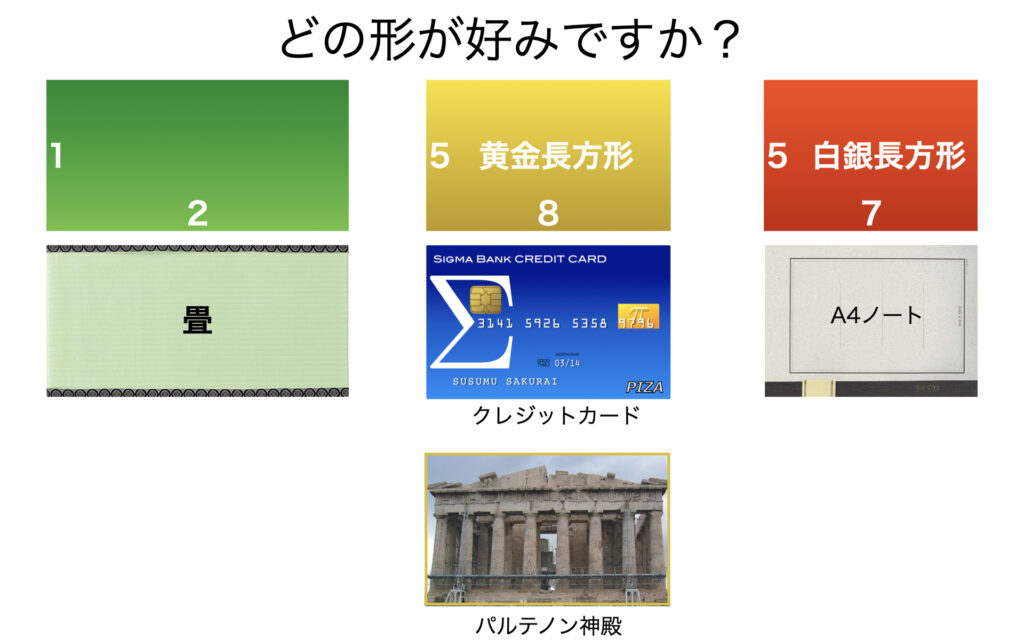
次の3つの長方形をパッとみたとき、どれが一番いいなと感じますか?直観で選んでみてください。

黄金比φ=1.6180399887…
真ん中の長方形を選んだ人はこの形をよく見ているからかもしれません。クレジットカードです。世界中、クレジットカード・銀行のカードの大きさは、横が85mm、たてが53mmと統一されています。それに合わせて、その他会員カードもそれとほぼ同じ大きさです。
たて・よこの比率を計算してみると、85÷53=1.603…です。黄金比は記号φ(ファイ)で表します。その値はφ=1.618…すなわち約1.6です。したがって、クレジットカードはほぼ黄金比でデザインされていることになります。
黄金比を100桁計算してみると次のようになります。
1.618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137
黄金比φは円周率πと同じように小数点以下が無限につづく数、無理数です。無理数とは、小数点以下の桁が循環することなく無限に現れる数のことです。
身のまわりに見つかる黄金分割・黄金長方形
1:φの比で線分を分けることを黄金分割、たて・よこの長さの比が1:φである長方形は黄金長方形と呼ばれます。φの小数第2位は1ですからこれを四捨五入した1.6は近似値として悪くない値です。1:1.6を整数比にしたのが5:8です。精度を要求しないのであれば黄金比は5:8として扱うのが便利です。
身のまわりには、黄金分割と黄金長方形がみつかります。液晶ディスプレイの画角には1920ドット:1200ドットのものがあります。これはぴたり1.6:1。ロゴマークをはじめ絵画・彫刻・建築といったデザインにも1:1.6はみつかります。

黄金比と相似
黄金長方形は次のような性質を持っています。まず、黄金長方形を1つ準備します。その短い辺を1辺とする正方形を黄金長方形からとりのぞくと小さい長方形がのこります。はたして、小さい長方形も黄金長方形となります。
他の辺の比の長方形ではこのようにはなりません。長方形から正方形を取り除いた小さい長方形がもとの長方形と辺の比が等しくなる(これを数学で相似という)特別な長方形が黄金長方形です。
黄金長方形から正方形を取り除いて小さい黄金長方形ができます。さらに小さい黄金長方形から同じように正方形を取り除けばやはりさらに小さい黄金長方形ができます。つまり、この作業を繰り返せば無限に大きさが異なる黄金長方形ができあがることになります。

黄金比の計算にチャレンジ
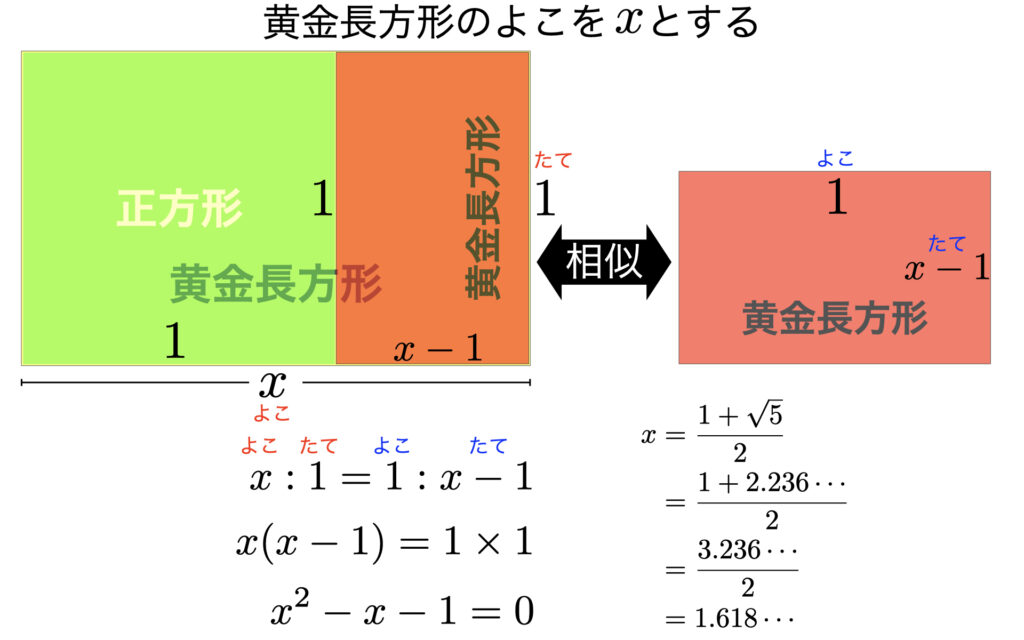
では実際に相似比の式を立てて黄金比を計算してみます。黄金長方形のたての長さを1、よこの長さをxとします。この黄金長方形から一辺の長さが1の正方形(図の緑)をとりのぞきます。すると、残りの小さい長方形は、たての長さが1で、よこの長さはx-1となります。
見やすくするためこの小さい長方形を90°回転したものを右に書き出します(図の赤)。もとの黄金長方形と小さい黄金長方形は相似になるので、よこ:たての比が等しくなります。それが、x:1=1:x-1です。
比例式の「内項の積=外項の積」より、1×1=x(x-1)が成り立ちます。これを整理すると、2次方程式 x²-x-1=0が得られます。2次方程式の解の公式を用いてxについて解けば、x=1.618…が求められます。
正五角形には黄金比が隠れている
黄金比の興味深い点はいろいろなところに現れることです。正五角形の中に黄金比が見つかります。ポイントは正五角形の中にある相似な三角形です。
相似な図形では、対応する辺の長さの比が等しくなります。その関係から辺の長さについての2次方程式が成り立ち、解くことができます。正五角形の1辺の長さを1、対角線の長さをxとするとxの2次方程式が得られるのでこれを解くとx=φが得られます。

黄金比は美しいのか?
黄金比を使えばなんでも美しくはなりません。したがって、黄金比と美しさの関係を説明することは容易ではありません。パルテノン神殿、ミロのヴィーナス、ダ・ビンチのモナリザ、クレジットカード、キャラクターといった人がつくりだすデザインに黄金比が見つかります。さらに、正五角形をはじめフィボナッチ数といった数学の中にも黄金比が見つかります。
正五角形や黄金長方形の例にあるように相似から導かれるのが黄金比φです。調和の表現の1つが相似ですから、その意味では黄金比が美に結びついているといえます。
いずれにしても黄金比は特別な数であることは間違いありません。
最初の図で左(緑)を選んだ人は畳の和室が好きな人かもしれません。右(赤)を選んだ人は勉強が好きな人かもしれません。ノートの形だからです。実はノートは黄金長方形ではなく、白銀比でできた白銀長方形です。次回は白銀比について謎解きをしていきます。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






