
位置を表す数
前回、「(−1)を掛けると向きが反対になる」という説明をしました。この考え方を進めることで数の世界の捉え方を大きく変えることができるようになります。
前回の説明
-5+3なら(-5)+(+3)と考えて、「0から左に5だけ進み、次にそこから右に3進むと-2のところに行き着く」という具合です。数直線上において-5という数は原点から左向きに5だけ離れた点、+3という数は原点から右向きに3だけ離れた点を表すといえます。正負というのは「向き」を表していることがわかります。
数直線の考え方とは、数を点という図形で表す、すなわち可視化するというものです。「数直線上において-5という数は原点から左向きに5だけ離れた点」でいうところの−5とは数直線上の「位置」を表す数です。これを数学では座標と呼びます。
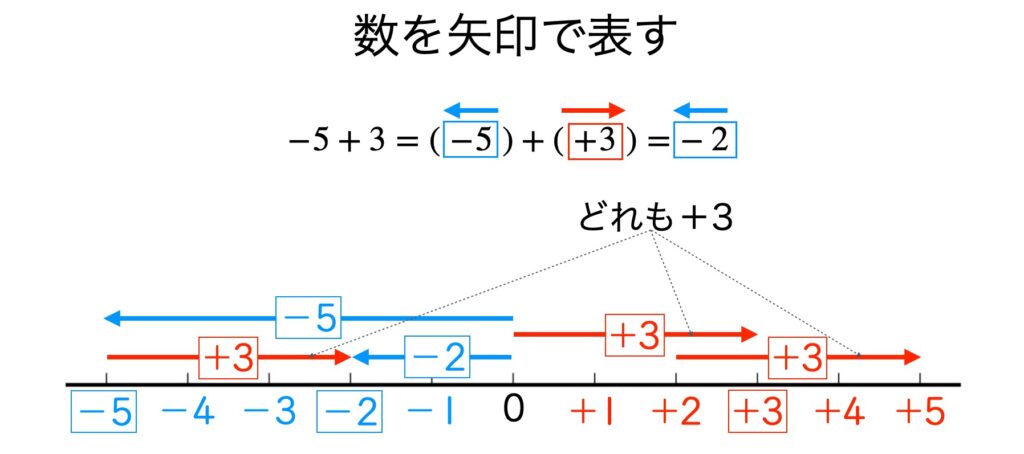
数を矢印で表す
これに対して「0から左に5だけ進み、次にそこから右に3進むと−2のところに行き着く」というように数には「向き」があると考えることができます。
「+3は原点から右に3だけ離れた点」「-5は原点から左に5だけ離れた点」ですが、これをそれぞれ「+3は長さ3の左向き矢印」「-5は長さ5の右向き矢印」と言い換えることで、正負の数の計算が矢印を使ってできます。+3の左向き矢印や-5はの右向き矢印は数直線上のどこにあってもかまわないところがポイントです。
かけ算を矢印で説明する
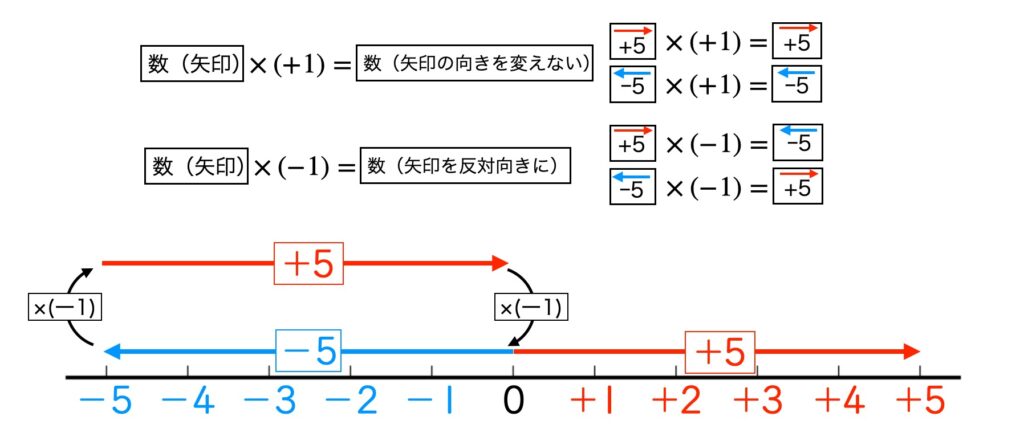
正負のかけ算もこの矢印を使って説明できます。(+5)×(+1)=+5という計算は、+5(左向き矢印)の長さを変えず、向きも変えない計算として答えが+5(左向き矢印)になります。
これに対して、(+5)×(-1)=-5という計算は、+5(左向き矢印)の長さを変えず、向きを反対向きにする計算として答えが-5(右向き矢印)になります。
「a×(+1)」はaの矢印の向きを変えない計算、「a×(-1)」はaの矢印の向きを反対向きに変える計算と説明できます。したがって、aを(-1)とすれば(-1)×(-1)の答えは、(-1)(左向き矢印)の向きを反対向きに変えるので(+1)(右向き矢印)になるということです。
ベクトルという考え方
矢印──大きさと向きを合わせ持つもの──を数学ではベクトルと呼びます。ベクトルは数のように計算できるのが特徴です。今回は正負の計算をベクトルで捉え直すことができることを紹介しました。これ以外にも数学の多くの分野はベクトルで捉え直すことできることからベクトルは数学の世界では基本かつ重要な考え方になっています。
物理学の世界では、速度や加速度といった量は大きさと向きを合わせ持つものなのでベクトルで表されます。経済学の世界では、価格ベクトル、生産量ベクトルといったように市場における量をベクトルで表すことで理論を組み立てることができます。
せっかく数を矢印(ベクトル)で表す考え方を知ったので、次回は新たな問題「虚数」の謎解きに応用してみましょう。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





