同じ数同士の積が負になるなんて!
前回、「マイナス×マイナスはなぜプラス?続編」を解説しました。謎解きのポイントは、数を矢印で表すという考え方です。今回はその考え方を使って、虚数の謎解きをしてみます。
imaginary number、直訳は想像上の数ですが、虚数と呼ばれます。頭文字のiが虚数を表す記号として用いられます。虚数iの最大の特徴は、「i×i=-1」に表されます。
最初にこれを見ると疑問符だらけになるでしょう。正の数×正の数および負の数×負の数、どちらも正の数になることから、私たちは「同じ数同士のかけ算(積)は必ず正」という結論(ルール)を得ます。
ところが「i×i=-1」はそのルールに反しているように思えます。同じ数同士の積が負になるなんて!どういうこと?
納得とは整合性があること
疑問は無理もありません。「どうして0乗は1になるの? 前編」、「どうして0乗は1になるの? 後編」、「マイナス×マイナスはなぜプラス?」では、(論理的)整合性のお話をしました。納得いくいかないは、整合性があるかないかのことなのです。
一見これまでのルールにあわないように思われる「i×i=-1」でも、そこに整合性があれば納得に変わるでしょう。「i×i=-1」にはどんな整合性があるのでしょうか。
数直線と数平面
数を点という形で表すことができます。それが数直線の考え方です。直線は点の集まりだからです。ならば、平面も点の集まりなので平面上の数を考えることもできるはず。ドイツの数学者ガウス(1777-1855)はそう考えて数の世界を直線から平面に拡張できることを示しました。それがガウス平面という考え方です。
数平面の横軸x軸と縦軸y軸にそれぞれ名前をつけます。数直線上にある数は実数と呼ばれる数です。そこから横軸を実軸と呼ばれます。不思議な虚数iはこの数平面の縦方向に現れる数です。そこで縦軸は虚軸と呼ばれます。
虚軸上には、-2i、-i、0、+i、+2iのように数が並びます。横軸(実軸)の1に相当するのが縦軸ではiということです。このiは虚数単位と呼ばれます。せっかくなのでもう一つ新しい用語を紹介します。
複素数です。+1+i、-2+2i、-3-iのように実数と虚数iを合わせた数です。英語では複合したという意味のcomplexを用いてcomplex numberと呼ばれます。数平面はガウス平面の他に複素平面、複素数平面などとも呼ばれます。

新しい用語がたくさん出てきましたが、ここでは「i×i=-1」だけにフォーカスしていきます。数を平面として考えるというアイディアだけを覚えてもらえればここから先のお話には十分です。
数の世界を直線から平面にすることは、数学にとって大きな変革になりました。その入り口を覗いていきます。
数平面上の数を矢印で表す
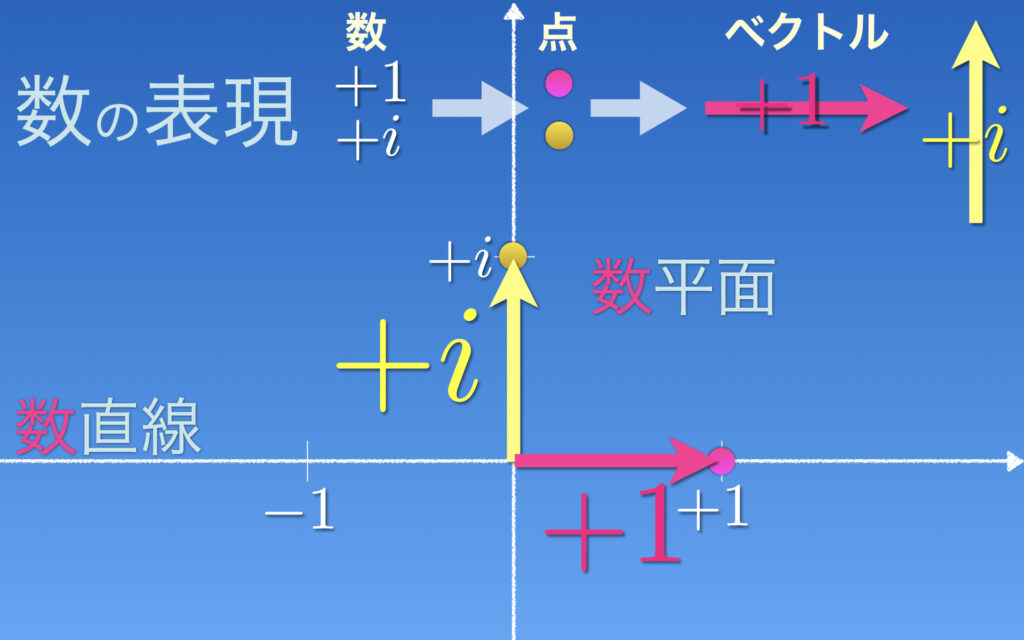
前回、数を矢印で表す考え方を紹介しました。これは数直線上でのお話でしたが、数平面でも同じように展開できます。数iは虚軸上の点(図の黄色の点)で表されます。数iを原点からその点を結ぶ縦向きの矢印↑(図の黄色矢印)とみることができます。
「虚数をかける」とは回転!?
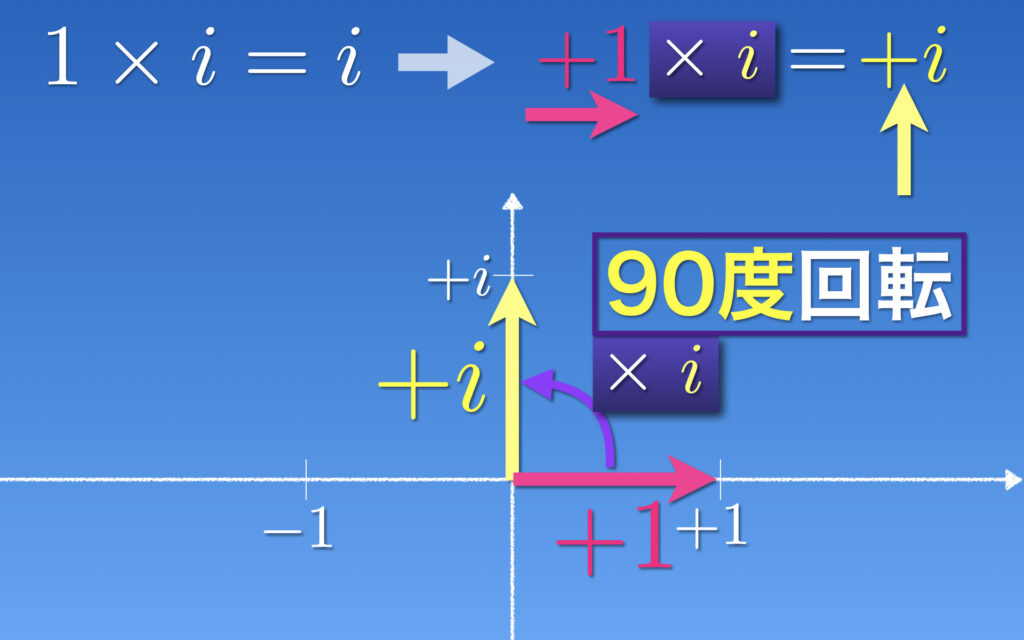
道具は揃いました。一気に「i×i=-1」に迫っていきましょう。最大のポイントは「×i」の解釈です。1×i=iという式は1の性質「1×a=a×1=a」から説明できますが、数平面上では次のように説明できます。
+1×i=+iとして+1は図の赤い矢印→、右辺の+iは図の黄色矢印↑です。すると、+1×i=+iは、→×i=↑となります。つまり、×iは矢印を反時計回りに90°回転すると解釈できます。
数i自体は虚軸上の点ですが、×iとなると数平面上での回転を意味することになります。
i×iを計算してみると
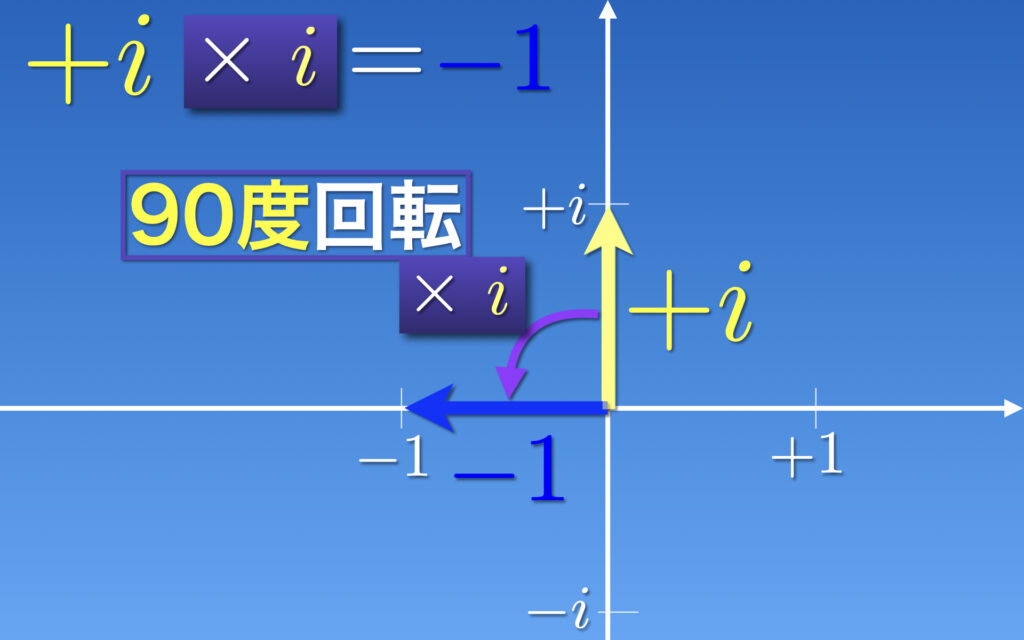
これですべての準備が整いました。i×i=-1を+i×i=-1とします。+iは図の黄色矢印↑ですから、+i×i=↑×i=↑を反時計周りに90°回転 = ← と計算できます。はたして←は数平面上の-1を表します。
「i×i=-1」が説明できました。通常、虚数iはi×i=-1を満たすような数だと説明されます。しかしこの説明からは整合性を読みとることは難しいです。×iは数平面上での回転を表すことができるという説明があれば、だいぶ納得できるはずです。
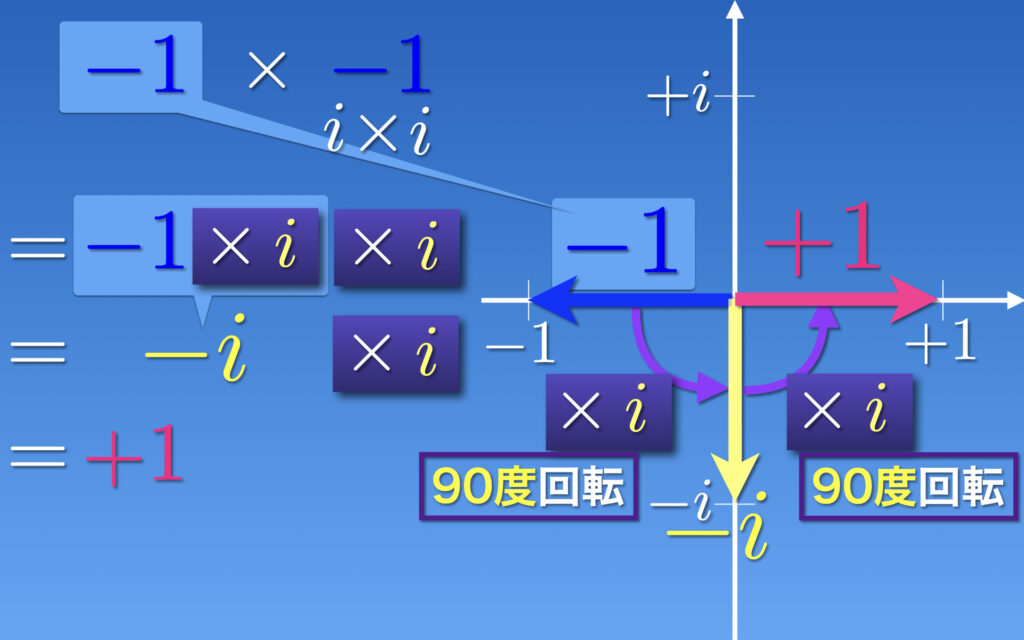
(−1)×(−1)を計算してみると
せっかくなので前回の「マイナス×マイナスはなぜプラス?続編」を虚数を使っても説明できることを紹介します。-1=i×iであることがわかったので、次のように数平面上の計算ができます。
(-1)×(-1)
= (-1)×i×i
= (-1×i)×i
= ↓×i
= →
= +1
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





