ノートに描かれた直線 ≠ 数学の直線
三角定規。図形の学習をする際に使う便利な道具です。三角定規と鉛筆でノートに描かれた直線は本当の直線ではありません。数学の直線ではないという意味です。数学における直線には幅がありません。ノートに描かれた直線には幅があります。この2つの直線の謎に迫っていきます。
小中高の算数・数学ではこのことにほとんど触れられません。知らない人がいても不思議ではありません。しかし、とても大切なことです。数学とはどういうものなのかを教えてくれるからです。
ユークリッドの『原論』
紀元前3世紀、古代ギリシャの数学者ユークリッドによって『幾何学原論』が編纂されました。古代ギリシャ数学を集大成した全13巻。20世紀初頭に至るまで数学の教科書として使われてきました。西洋では聖書に次いで世界中で読まれてきた本とされています。
第1巻冒頭を見てみましょう。
定義1 点は部分をもたないものである。
定義2 線には幅は無く長さがある。
定義3 線の端は点である。
定義4 直線とは点がまっすぐに並んだ線である。
定義5 面には長さと幅だけがある。
明確に線には幅は無いと書かれてあります。議論の前提となる点や線、直線、面などの意味を定める(明確に規定する)ことを定義といいます。定義4から、直線は点(定義1)と線(定義2)によって定義されることがわかります。
まさにここから数学がはじまりました。二千年もの間、数学の教科書として使われてきたことに驚かされます。
幅のない線の実例 アルキメデスのアイディア
分かりづらい「幅のない直線」を説明するのに格好な例がユークリッドの時代に活躍した数学者アルキメデスです。算数の教科書で円周率を学びます。円には「直径と円周の長さの比が円の大きさによらずに一定である」という性質があります。この比が円周率で記号πで表され、その値は約3.14であることも習います。
アルキメデスはπが3.14であることを次のようにして突き止めました。直径1の円に対して、内接正6角形と外接正6角形を考えます。すると、直径が1なので円周の長さが円周率になるので、次のような関係が成り立ちます。
内接正6角形の周の長さ<直径1の円周(円周率)<外接正6角形の周の長さ
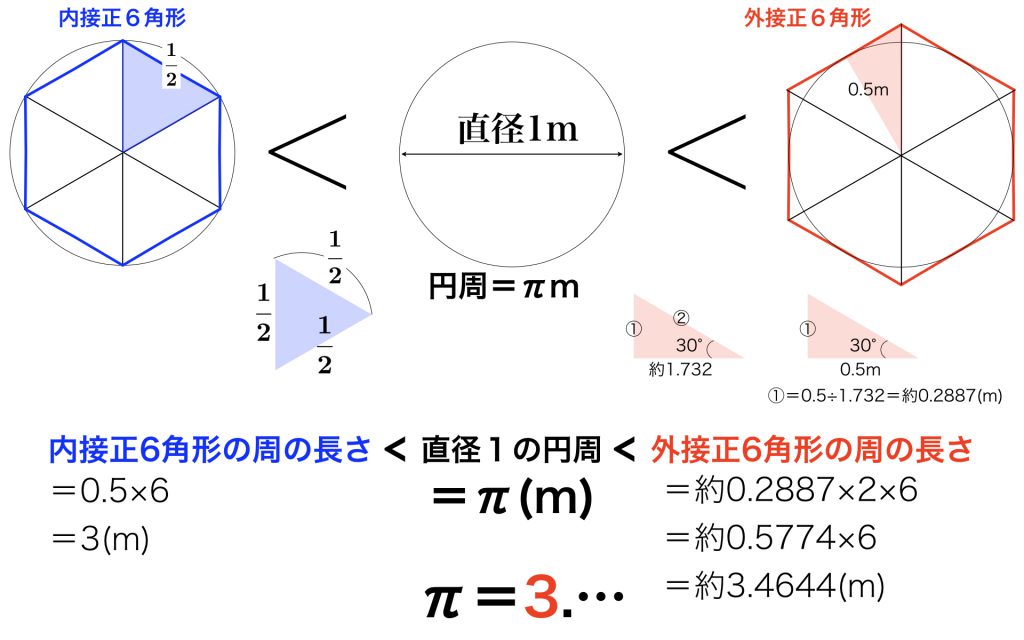
正6角形ではπ=3.???としかわかりません。もっと角数を大きくすることで正多角形の周の長さは円周に近づきます。だからと言って単純に角数を大きくしてもその周の長さを得ることは容易ではありません。
アルキメデスは、円に内接および外接する正6角形から始めて正12角形、正24角形と倍々にしていくことで、内接および外接正多角形の周の長さが”分かる”ことを発見しました。
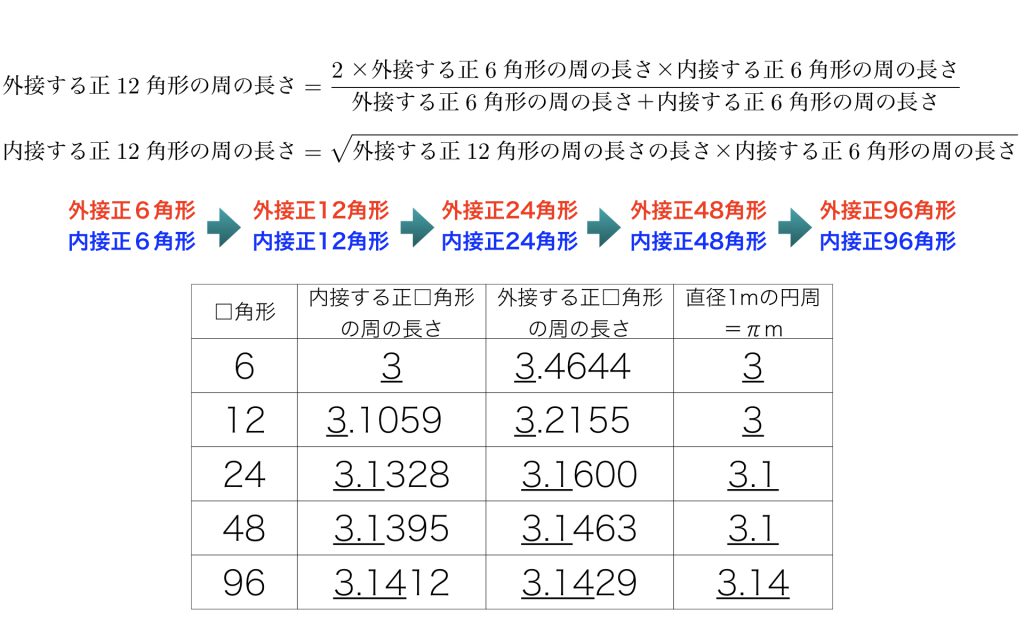
内接正6角形と外接正6角形の周の長さから内接正12角形と外接正12角形の周の長さが”分かり”、内接正12角形と外接正12角形の周の長さから内接正24角形と外接正24角形の周の長さが”分かる”というアイディアです。
この倍々を正96角形まで続けることでついに、π=3.14…であることがわかりました。

アルキメデスが考えた正96角形。実際にアルキメデスはノートに鉛筆で描いたのでしょうか。不可能です。アルキメデスは頭の中に正96角形を描きました。その図形の線の幅がゼロだということです。頭の中であればどんなに大きな正多角形でも描くことが可能です。
数学とはイデアの世界
数学が扱う直線とは、鉛筆でノートに描いたものではなく、頭の中に描かれたものだということです。これを概念といいます。ユークリッドは『原論』の中で、点や線の概念を定義しました。
数学とは概念の世界を探求する学問です。天文学や物理学はお星様の世界(モノの世界)を探究します。ノートに鉛筆で描かれた直線は炭素というモノとしての存在です。顕微鏡で覗けば炭素の粒々が見えます。それに対して数学の直線は幅がないので目に見えない存在でこの世には存在しません。
概念はイデア(idea)とも呼ばれます。目に見える直線と見えない直線の関係と同じ例が数字と数です。【連載:数学と言葉】第2回 数の言葉使いその2 数と数字のちがい説明できますかでも取り上げたように、数は概念(イデア)で目に見えない存在、数字はシンボルで目に見える存在です。
アルキメデスは法則を発見したことにより円周率πに迫ることができました。「内接正12角形と外接正12角形の周の長さから内接正24角形と外接正24角形の周の長さが”分かる”」の分かるとは計算できることを意味します。図形と数はどちらもイデアの世界です。イデアの世界に隠された法則を発見するのが数学者の仕事というわけです。
数学は目に見えない存在だから何にでも役立つ
数学ほど役に立つものはありません。
それは数学がイデアすなわちアイディアの存在だからです。AI時代を生き抜く新しい数学力 第1回 新しい数学の学びの時代でも紹介したように、地図をつくるのも、コンピューターをつくるのにも、そして現在のAI(人口知能)技術も数学によってつくられています。
幅がない目に見えない直線を考えたことで、文明が発達してきたということです。筆者がよく例に出すのはカーナビです。地球を周回しているGPS衛星からの電波を地上の車はキャッチすることで現在位置を知ることができます。ピタゴラスの定理(三平方の定理)をはじめとする数学によってデータの計算処理が行われます。
中でも人工衛星の速度が大きいことと地球からの重力を受けることの影響を計算するのがアインシュタインの2つの相対性理論です。相対性理論の計算のおかげで誤差を小さくし精確な位置を算出できます。
重力の影響を計算する一般相対性理論は幾何学の集大成のようなものです。最初に見た『原論』の定義が二千年後に役立っているということです。
数学は目に見えない存在だから難しい
数学の正体は概念(イデア)ですが、それを表す言葉・シンボル(図形や文字)が必要です。それがなければ数学を表すことができません。ノートに鉛筆で描かれた直線、教科書に印刷された直線、どちらも本当の直線ではないことを念頭に置くことが大切です。
とはいえ目に見えない存在を理解することは想像以上に難しいことです。人類が数学を手にして数千年しか経っていません。数学は目に見えないということを知っただけではほとんど役に立ちません。
第9回 世界の難しさを知る力 数学の“ムズカシサ”から“難しさ”へ
もしノートや教科書、黒板に描かれた直線を本当の(数学の)直線と勘違いしてしまうと数学自体が分からなくなってしまう恐れがあります。自身の頭脳で目に見えない直線をみようとするトレーニングを積み重ねることではじめて獲得できます。
新たな疑問
定義3 線の端は点である。
定義4 直線とは点がまっすぐに並んだ線である。
から、直線は点でできていることになります。
ところで
定義1 点は部分をもたないものである。
とは、点には長さも幅も厚さもないということ、つまり点の大きさはゼロということです。
したがって、
大きさがゼロの点が集まって長さがある直線ができる
ということになりますが、どう理解すればいいのでしょうか。これは難問です。いずれ本連載で解説します。それまで考えてみてください。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





