映画「おもひでぽろぽろ」(高畑勲監督・脚本、1991年スタジオジブリ)のワンシーン
ヤエ子:分母と分子をひっくり返してかけりゃいいだけじゃないの。学校でそう教わったでしょ。
タエ子:う〜ん。
ヤエ子:じゃあ、どうして間違ったの。
タエ子:分数を分数で割るってどういうこと?
3分の2個のリンゴを4分の1で割るっていうのは、3分の2のリンゴを4人で分けると一人何個かってことでしょ。
だから、いち、に、さん、し、ご、ろくで、一人6分の1個。
ヤエ子:ちがう、ちがう、ちがう、ちがう。それはかけ算。
タエ子:え〜、どうして。かけるのに数が減るの。
ヤエ子:3分の2個のリンゴを4分の1で割るっていうのは、……。とにかく、リンゴにこだわるからわかんないのよ。かけ算はそのまま、わり算はひっくり返すって覚えればいいの。
主人公タエ子(小5)と姉ヤエ子との会話です。
タエ子は分数の割り算を考えて理解しようとしているのに対して、姉は計算手順を必死で覚えさせようとしています。
30年経った現在でも、分数の割り算が置かれた状況は変わっていません。この二人の主張はどちらも正しいといえます。なぜ分数の割り算は分母と分子をひっくり返してかけ算としていいのかという疑問は当然です。はたして、その理解となると容易ではないことも事実です。計算手順を公式として覚えることはダメなことではありません。
数学の公式を理解しないとダメとしてしまうと前に進むことが難しくなります。結果として数学の学び自体が停止しかねません。「信じる者は救われる」の精神で、公式をとにかく使い続けてみる(覚えることを優先にしてしまうのはダメ)ことで数学の感触を獲得していくことが大切です。算数・数学の「なぜ」は大切に温存しつつです。
数学の考え方の実力が身についてきたならば「なぜ」にチャレンジしてみるということです。今回のテーマの分数の割り算は、きっと大学生になったとしてもじっくり考える時間はないのが普通です。
ではいつチャンスはやってくるのか。親となり自分の子供が小学生になった時です。27歳で結婚したとして、34歳で子供が小学1年生、40歳で小学6年生になります。その時がチャンスです。小6の子供といっしょに分数の割り算を考えてみましょう。そのときのためにヒントになることをこれからみていきます。
分数の割り算の公式を納得する計算その1
ちゃんとした「公式」の理解は最後にまわします。それまでに、公式を使って納得する計算をいくつか取り組んでみます。最初の計算は明らかに簡単な2つの数の割り算を取り上げます。
4÷4=1の割り算をあえて分数どうしの割り算に変換し、「公式」を使って計算してみます。それでも確かに1となります。なるほど「公式」の正しさが納得できます。

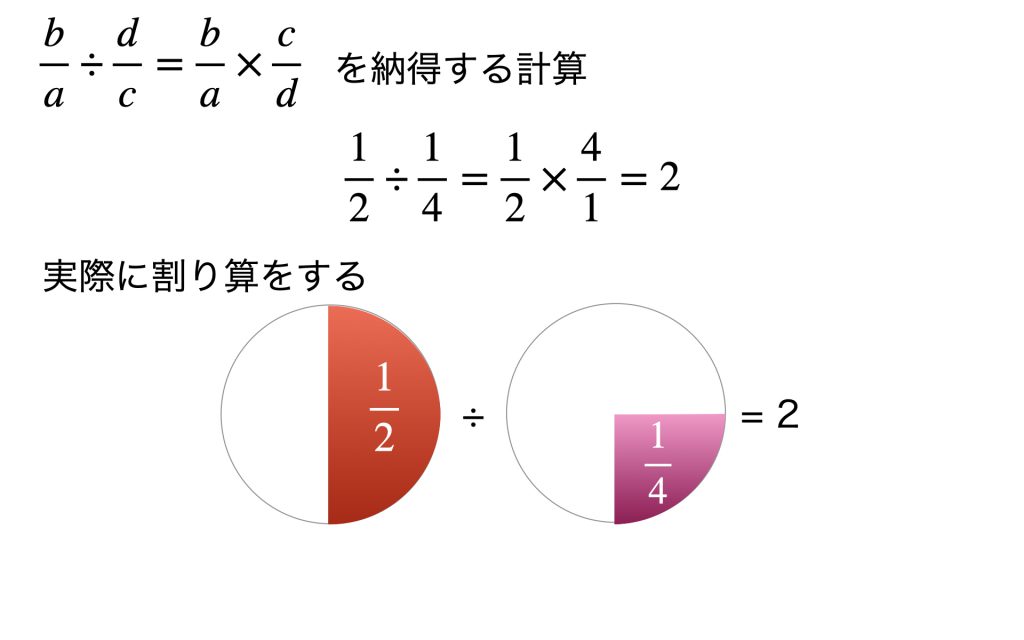
分数の割り算の公式を納得する計算その2
その1と同じように簡単な例で分数の割り算をしてみます。1/2÷1/4を「公式」に従って計算すると答えは2となります。全円の大きさを1とすれば1/2、1/4はそれぞれ半円、4分の1円となり図示が容易です。1/2の中に1/4は2つあることは明らかです。「公式」の妥当性を確認できます。
「公式」を理解するための準備「÷(1/b)→×b」
整数(自然数)で割ることは実例により理解は容易です。それが分数で割るになると状況が一変します。そもそも日常の中で分数で割るような場面は滅多にありません。仕方がないので最後に無理に分数で割る問題を作って考えることにします。
1/bのように分子が1の分数で割ることが基本になります。次の図のように説明することで、÷1/4が×4に等しいことがわかります。
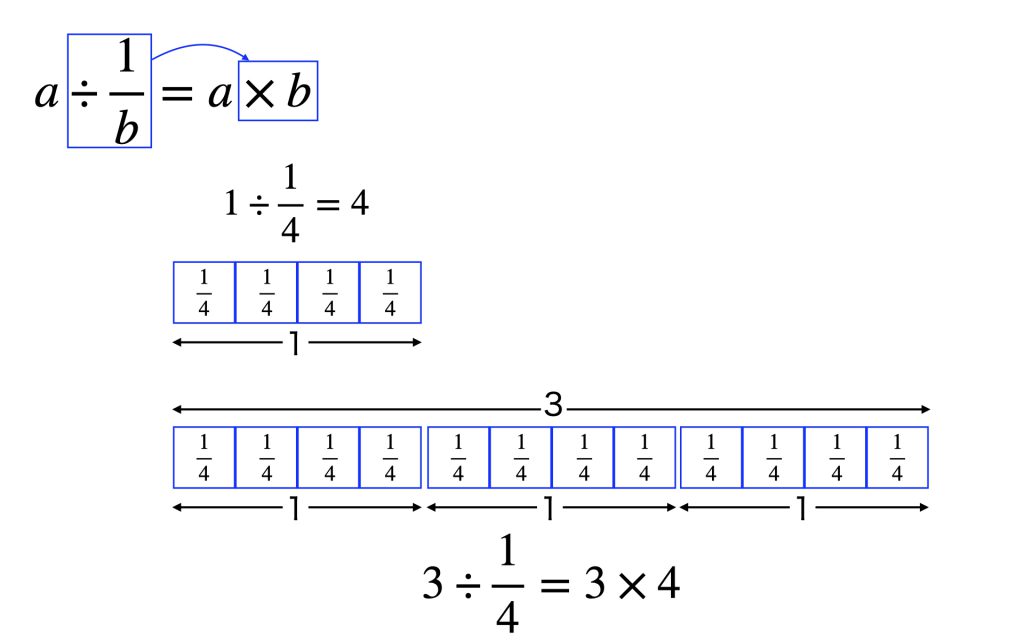
「÷(1/b)→×b」がわかれば、冒頭のタエ子に対する解説もできます。
÷1/4は×4だから2/3÷1/4 = 2/3×4 = 8/3
実際に割り算する
これで終わりにしてもタエ子には不満が残るかもしれません。そこでダメ押しの解説を考えてみましょう。タエ子はリンゴの絵で考えていました。本当に割り算をしようとしていたのです。
それに応えてあげます。コツはズバリ、通分!
通分は分数のたし算・ひき算で習いますが、実は割り算にも使えます。2/3と1/4を通分すると分母は12(3×4)です。そこで全円を12等分した図を描きます。その図で2/3=8/12と1/4=3/12を考えます。
8/12の図形に3/12である4分の1円が何個含まれるかを考えると、2個とショートケーキの形です。ショートケーキの形は1/12が2つ分なので4分の1円を1個とすれば2/3個です。したがって、答えは2+2/3=8/3。
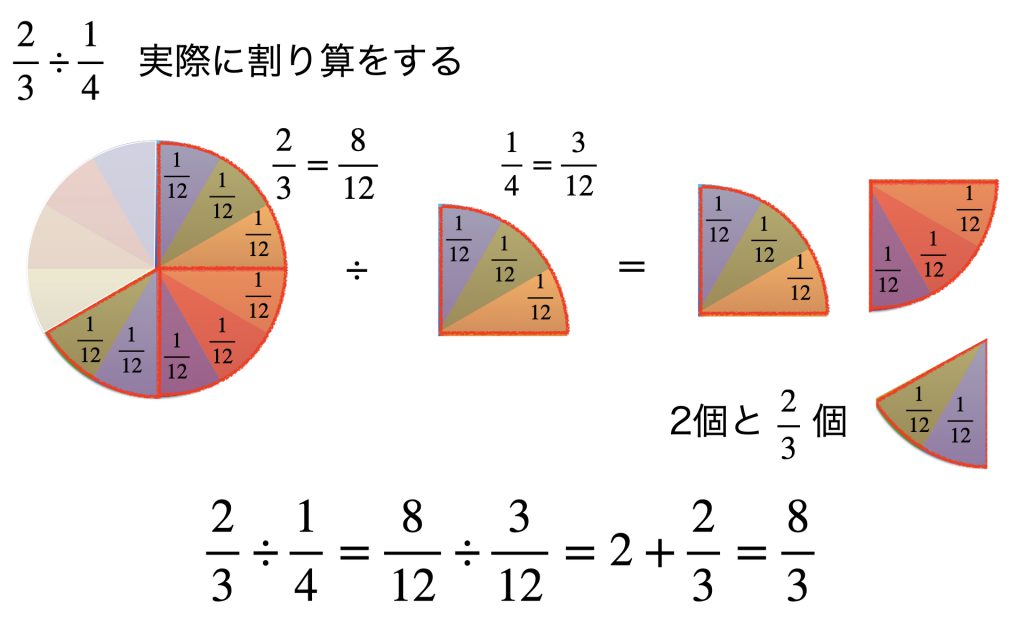
せっかく通分したので、2/3÷1/4 = 8/12÷3/12から分母が等しい場合、割り算は分子どうしの割り算8÷3に等しいことも説明できます。

「公式」に迫る 「困難は分割せよ」
タエ子の問題は割る分数が1/4なので「÷(1/b)→×b」が分かればOKです。次は分子が1でない場合です。÷5/7が×7/5になることを見ていきます。
まず、5/7を5×1/7と2つに分けます。これが「困難は分割せよ」のことです。a÷(b×c)=(a÷b)÷c が成り立ちます。12÷6=2を例に説明してみると、6=2×3なので、まず12を2で割り、次に3で割るということです。
÷5/7 = ÷(5×1/7) = ÷5 ÷1/7
ここで、÷5 = ×1/5 は問題ありません。÷1/7 は「÷(1/b)→×b」より×7に置き換えることができるので、
2/3÷5/7 = 2/3×1/5×7 = (2×7)/(3×5) = 14/15
と計算できます。

最後に両辺を小数で計算して確かめておきます。
2/3÷5/7 = 0.6666666… ÷ 0.7142857… = 0.933333…
14/15 = 0.933333…
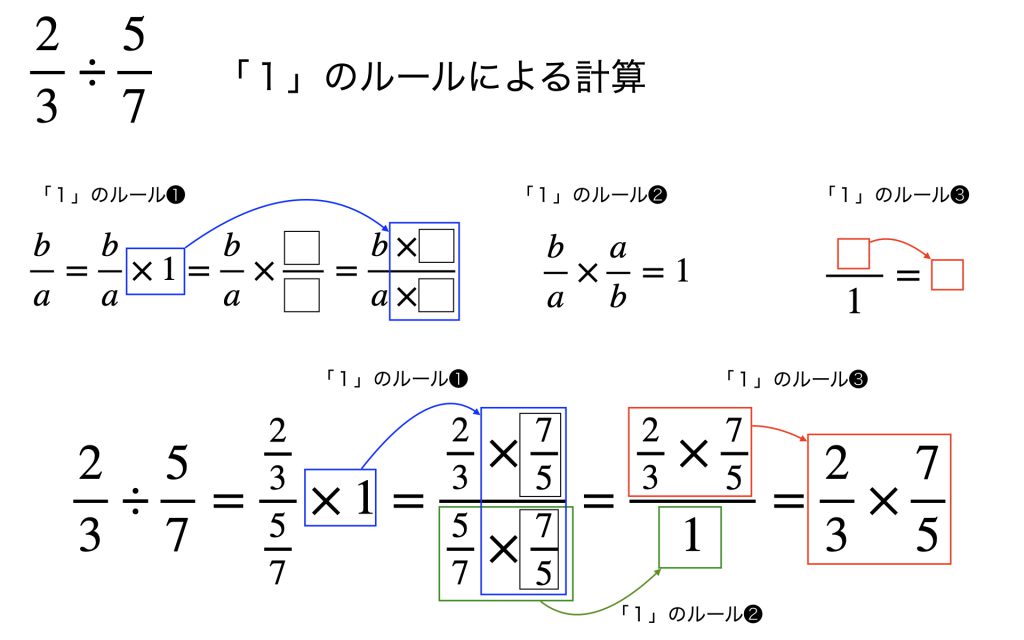
「公式」に迫る 「1」のルール
同じ問題について別な計算方法を考えてみます。3つの「1」のルールです。
「1」のルール❶
a/bに1をかけても値は変わりません。この1を分数/分数(2つの分数は等しい)としてしても値は変わりません。
a/b = (a×分数)/ (b×分数)
「1」のルール❷
b/a×a/b = 1
これは分数どうしのかけ算のルールで説明できます。
「1」のルール❸
a/1=a
分母が1であれば分子に等しいということです。
以上の3つを使うことで2/3÷5/7=2/3×7/5が説明できます。
「公式」に迫る 単位量の変換
問題 7/5リットルで1メートル塗ることができるペンキがあります。2/3リットルでは何メートル塗ることができますか。
これが、分数÷分数となるように無理につくった問題です。問題のための問題であることには目を瞑って、お付き合いください。最後に大切なことがわかります。
(割り算の解法) 2/3 L÷7/5 L/m = ?m が自然です。ここで分数の割り算が問題になります。分数の割り算が分からないとしたらどうしたらいいでしょうか。
問題のペンキは7/5リットルで1メートル塗ることができるものです。これを1リットルでは何メートル塗ることができるのかが分かれば計算ができます。
1リットル → □ メートル
2/3リットル → ? メートル
という関係から(かけ算の解法)?=2/3×□ と計算できます。一旦、1メートル当たりの塗ることができる長さを求めるということです、
図を描いて考えるとわかりやすくなります。図のように赤い帯の長方形を7等分します(右の長方形)。1つ分の短冊が1/7m、1/5Lとなります。1Lは短冊5つ分(1/5L×5=1L)なので、長さは1/7m×5=5/7mとなります。これが求める1メートル当たりの塗ることができる長さです。
したがって、(かけ算の解法)2/3×5/7 =10/21 答え10/21m。

割り算とかけ算の解法について数値に単位をつけて比較してみます。
(割り算の解法)2/3 L÷7/5 L/m = ?m
(かけ算の解法)2/3 L×5/7 m/L = 10/21 m
7/5 L/m は1m当たり7/5Lであること、5/7 m/Lは1L当たり5/7mであることを表しています。単位量を入れ替えると、数値は分母と分子をひっくり返すことになり、計算は割り算とかけ算が入れかわるということなのです。
ガソリン価格1リットル当たり120円
円ドル為替1ドル140円
牛肉100グラム当たり1800円
金相場1グラム当たり7762円
といった単位量に日常で接します。しかし残念ながらこれを単位量変換する機会はほとんどありません。分数÷分数といった分数の割り算の問題自体、日常で見つけることは容易ではありません。
もしペンキの問題に代わる(分数÷分数の)いい例題を見つけられたなら面白いでしょう。小学生をもつ親になって分数の割り算の問題に取り組むときまで、ぜひ例題探しをしてみてください。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





