数学の教科書に登場する√の計算、電卓にも√キーがあります。普段の生活の中で使うのは四則(+−×÷)がほとんどで√の計算をする機会はないように思われます。しかし、意外に身近なところに√の計算は隠れています。

√の計算その1 コピー用紙の縦横比
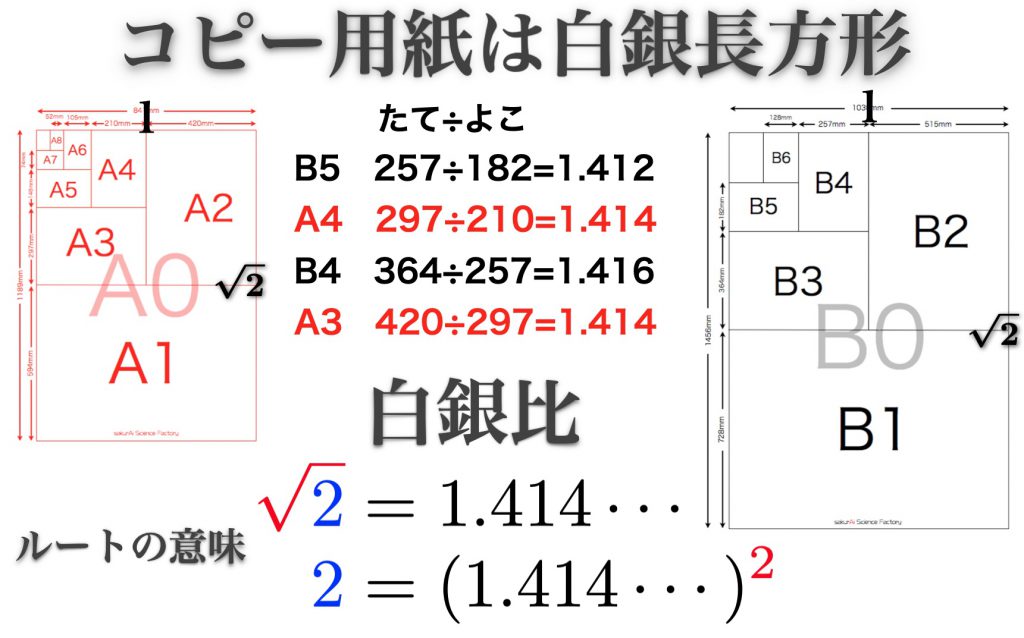
ノートやコピー用紙は縦横の比が白銀比でできた白銀長方形です。コピー用紙は半折りにしても相似である(形が変わらない)ようデザインされています。コピー用紙は縦に半折りにすると面積は半分になりますが、縦横比が変わりません。このような性質を持つ長方形の条件は、横1に対して縦√2の場合です。
√2はSilver Ratio、白銀比と呼ばれています。白銀比の長方形を白銀長方形といいます。白銀長方形だけが半折りにしても相似になります。コピー用紙や本の判型は白銀長方形でデザインされています。
A4版は297mm×210mmです。電卓で縦横比を計算してみると297÷210=1.4142857です。続いて、√2=1.4142135を確認してみます。両者は5桁合致していることに驚かされます。
B5、B4、A3でも同じように縦横比を計算してみると1.41か1.414であることが確認できます。白銀比と呼ばれる√2のおかげでコピー用紙は機能的にデザインされているということです。
ちなみにA版は国際規格ですが、B版は日本独自規格です。なぜ日本にはこの2つの規格があるのでしょうか? その謎解きは改めて紹介します。
√の計算その2 日本建築の曲尺
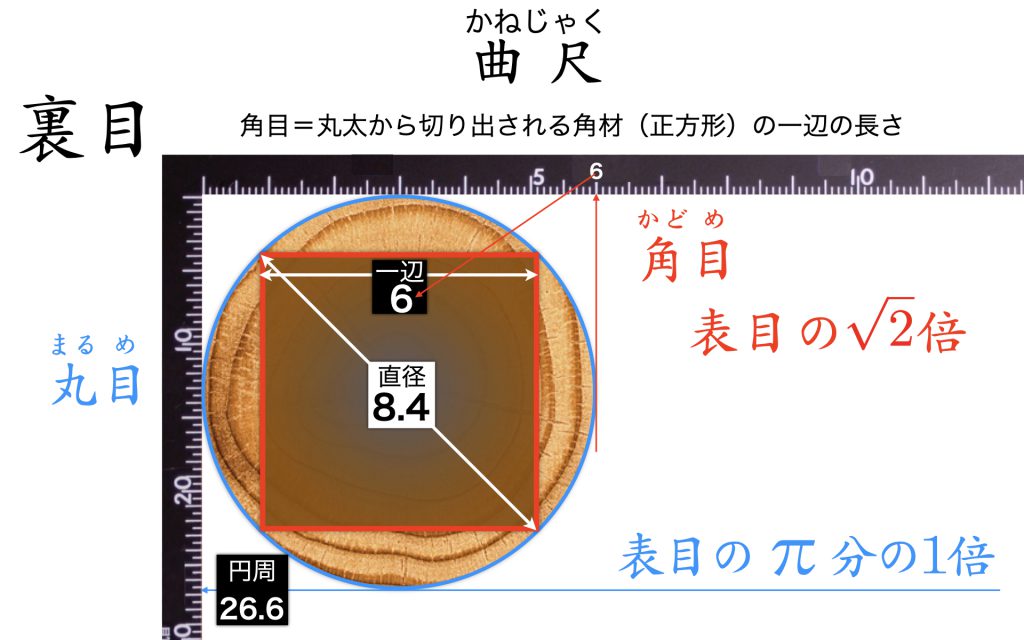
日本建築で大工さんが使う曲尺(かねじゃく)には表目と裏目があります。表目は一般の定規と同じ目盛りがふってあります。曲尺の最大の特徴は裏目です。裏目の短い方を丸目、長い方を角目といいます。
日本では切り出された丸太から角材を切り出します。丸太の状態で断面が正方形の角材の一辺の長さと周の長さを知ることができるのが角目と丸目です。図のように曲尺で丸太を測る場合、丸太のへりが指す角目の値が角材の一辺の長さ、同じく丸目の値が丸太の周の長さに相当します。
丸太を裏目で測ると、切り出される角材の一辺と丸太の周の長さが一目でわかるということです。角目、裏目にはそれぞれ白銀比√2、円周率π(=3.14…)が仕込まれています。
曲尺を手に取る機会があったら、表目と裏目の目盛りの間隔が違うことを確かめてみてください。
√の計算その3 試験の成績 偏差値と標準偏差
母集団が大きな模擬試験では、個人成績表には得点、平均点、順位、そして偏差値が記載されています。都道府県や全国規模の入学試験では、数値化された偏差値によって高校・大学のランキングを知ることができるので受験者にとって大変便利です。
得点も偏差値も同じ数値ですが、意味が違います。どちらも2桁なので偏差値を得点と同じようなものだと勘違いする人がいても不思議はありません。偏差値の求め方を知ることで得点と偏差値の違いもわかります。
ランキングを得点や順位だけで比べることには無理があります。簡単な試験と難しい試験を得点だけで比べても意味がありませんし受験者数が異なる順位で比べるのも容易ではありません。偏差値によりランキング(受験者全体の中での位置)を知ることができます。次が偏差値を求める公式です。
偏差値の公式
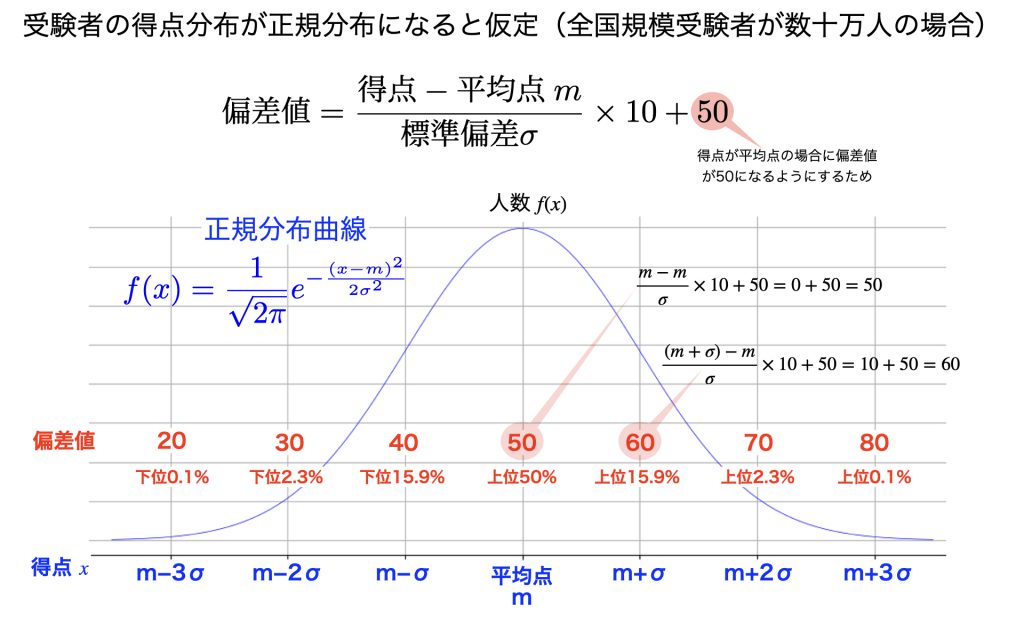
(偏差値)=(得点−平均)÷(標準偏差)×10+50
平均は点数の合計を人数で割った値です。誰でも簡単に計算できます。それに対して標準偏差はあまり良く知られていません。標準偏差とは、ばらつきを表す指標です。標準偏差が大きいとばらつきも大きく、標準偏差が小さいとばらつきも小さいということです。
偏差値の公式の最後にある「+50」とは、得点が平均点の場合に偏差値が50になるように設計されていることを意味します。偏差値60とは受験者全体の上位15.9%に位置していることを意味します。偏差値70は上位2.3%です。
偏差値が70というのがいかに成績上位かということです。偏差値70は70点ではないということです。
ところで、偏差値では母集団の数が重要です。全国40万人が受験するような試験ではその分布が正規分布に近くなるので偏差値は意味を持ちます。しかし、1学級40人で偏差値を計算したところでそもそも得点分布は正規分布にはならないので偏差値は意味をもちません。
正規分布とは、平均に最も多く人数が集中し、満点や零点に近づくほど少なくなる分布です。分布図は左右対称で釣り鐘型になります。
この標準偏差の求め方の中に√が登場します。標準偏差は、各受験者の「得点−平均点」を2乗し、全員分足して、さらに受験者数で割った数の平方根をとった数値です。AさんからFさんの6人分の得点から標準偏差と偏差値を計算してみましょう。電卓の√キーの出番です。

コピー用紙、曲尺、偏差値の中に隠れている√を紹介しました。読んで知っただけでは「ふ〜ん、そうなんだ」止まりです。電卓の√キーを叩いて自分の目で確かめてみることで「本当だ!」「ほんまや!」と驚きにかわります。
後編に続く。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





