
中学入試問題にチャレンジその1

フィボナッチ数はたし算だけで理解できるので中学入試にも取り上げられます。2003年の東京学芸大付属竹早中学校入試問題は、フィボナッチ数を知っていれば問題がフィボナッチ数そのものだとわかるものです。
解答
(ア)3+5=8
(イ)13+21=34
中学入試問題にチャレンジその2

次は1998年の東京女学館中入試問題です。問題がフィボナッチ数であることに気づくかどうかがポイントです。
階段が1段、2段、3段そして4段までは実際に階段の図を描いてのぼり方を列挙していけばわかります。しかし、7段となると階段の図を描いてのぼり方のすべてを列挙することは容易ではなくなります。
まず、問題をたし算の表し方であることに言い換えることができればわざわざ階段の図を描くことなく計算だけで考えることができるようになります。すると、5段の場合を考えてみると、
(1+1+1+1)は4段の場合ののぼり方になるので5通りとわかります。
次に、最初の1歩が2段の場合、
(1+1+1)は3段の場合ののぼり方になるので3通りとわかります。
したがって、合計5+3=8通りと計算できます。
n段ある階段ののぼり方は最初の1歩は1段か2段です。
・最初に1段の場合ののぼり方は、n-1段の場合ののぼり方
・最初に2段の場合ののぼり方は、n-2段の場合ののぼり方
となることがわかります。したがって、
フィボナッチ数がつくる形
フィボナッチ数1、1、2、3、5、8、13、…から面白い形をつくることができます。はじめに半径1の4分の1円を描きます。そこから続けて半径1の4分の1円を描きます。そこから続けて半径2の4分の1円を描きます。という具合にフィボナッチ数を半径とする4分の1円を描いていくとらせんの形が現れます。
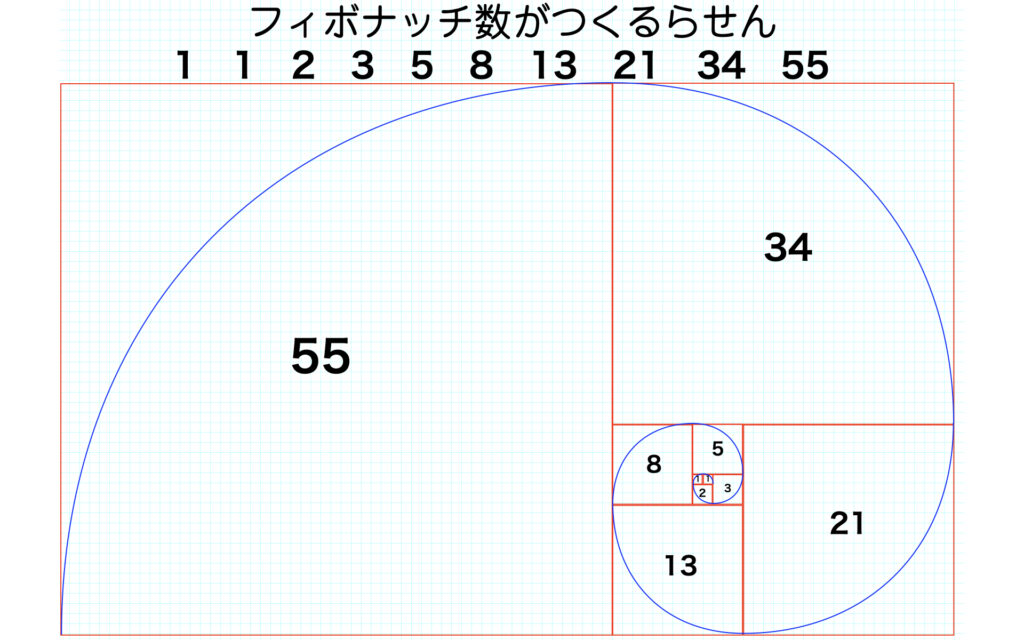
らせんの形は自然界に見つけることができます。オウム貝、台風、銀河など。らせんをモチーフにしたらせん階段やペーズリー柄の洋服などがデザインされています。

松ぼっくりとひまわりに見つかるフィボナッチ数とらせん
身近にある植物の中にフィボナッチ数とらせんを見つけることができます。松ぼっくりの一枚一枚の鱗片をよく観察してみると左回りのらせんと右回りのらせんがあることに気づきます。
興味深いことに左回りのらせんは8本、右回りのらせんは13本でフィボナッチ数に一致しています。

同じようにひまわりの一つ一つの花をよく観察してみると左回りのらせんと右回りのらせんがあります。すると、左回りのらせんは55本、右回りのらせんは34本でこれもフィボナッチ数に一致しているではありませんか!
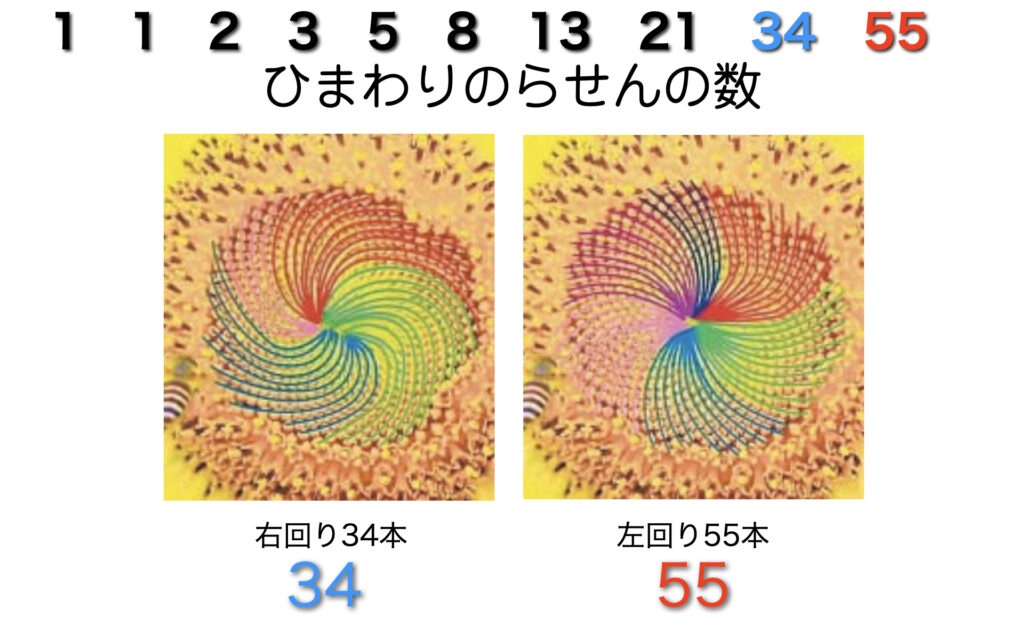

ぜひご自身の目で確かめてみてください。きっと驚かれることでしょう。
中学入試問題にチャレンジその3

2004年の実践女子学園中入試問題はずばりフィボナッチ数とらせんの問題です。
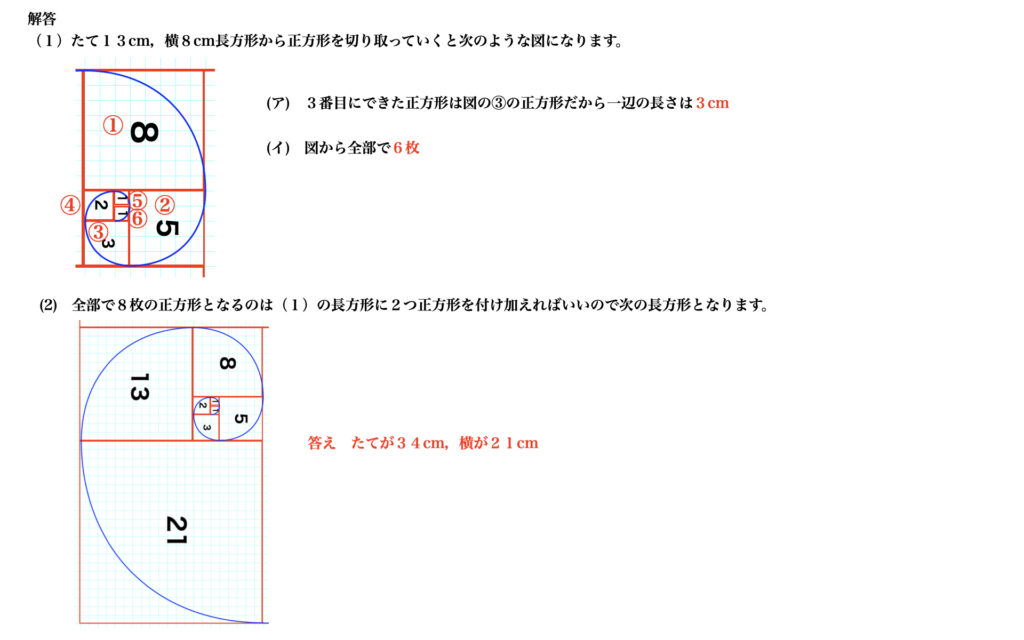
このように入試問題や身近な植物にフィボナッチ数が隠れています。ぜひ方眼紙にフィボナッチ数からつくられるらせんを描いてみましょう。大きな方眼紙を使うことをおすすめします。
次回はフィボナッチ数を使った「フィボナッチ・マジック」を紹介します。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






