
九九はすべて覚えなくてもいい!?
前回は九九の九の段が両手の中にあることを紹介しました。実はそれ以外の九九も両手で計算する方法があります。5以下×5以下の九九さえ覚えれば、5以上×5以上の九九が計算できてしまいます。
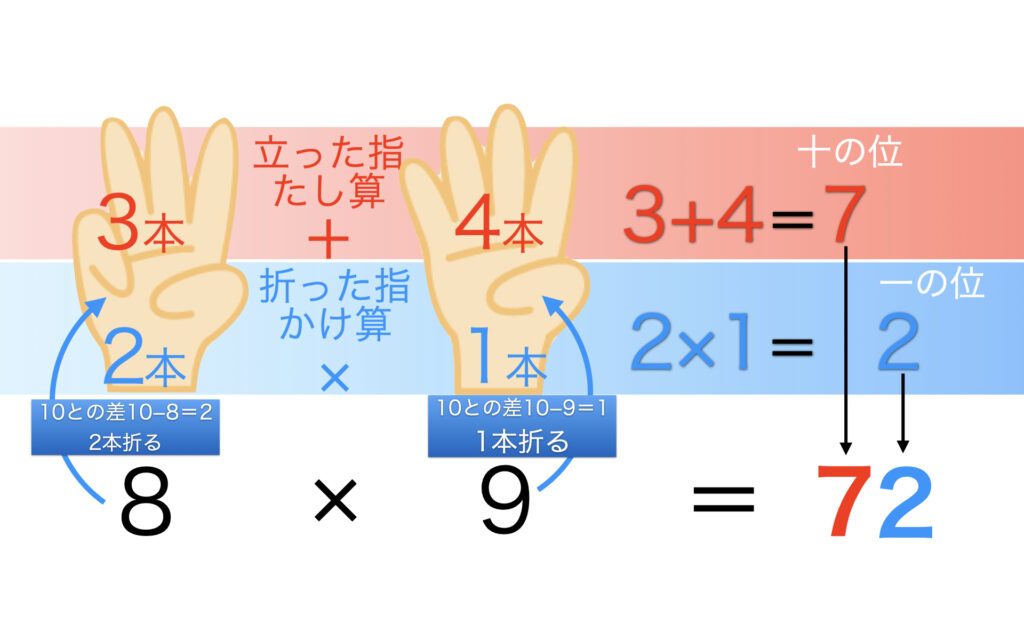
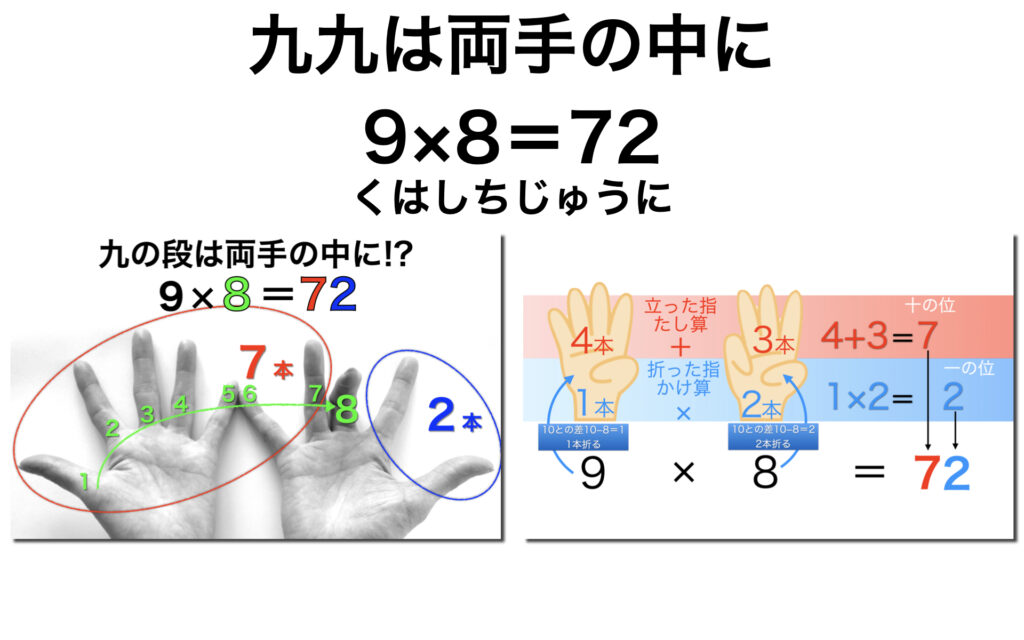
8×9であれば、左手で8、右手で9を表します。10との差だけ指を折ります。8は10との差は2、9は10との差は1なので左手は2本、右手は1本指を折ります。これで準備OK。10に足りない数だけ両手の指を折ります。
両手の指を折ったまま、両手をくっつけます。立っている指の合計を数えます。左手は3本、右手は4本立っているので3+4で7です。これが答えの十の位です。次に、両手の折っている指の数同士をかけます。左手は2本、右手は1本なので2×1で2です。これが答えの一の位です。この7と2を合わせて8×9が72とわかるという計算方法です。
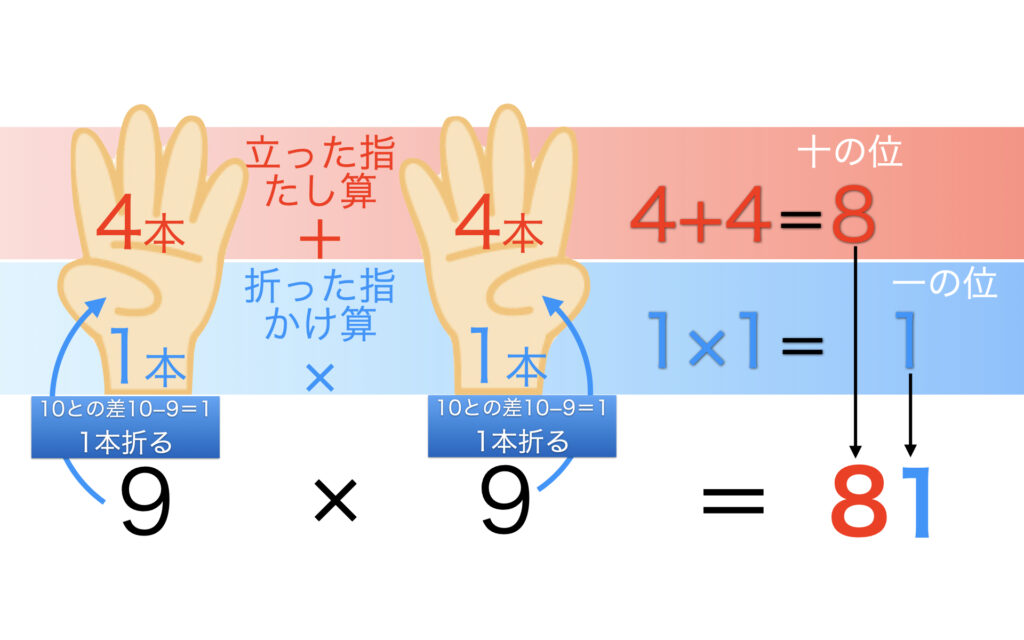
9×9=81の場合
左手で9、右手で9を表します。10との差だけ指を折ります。9は10との差は1なので左手も右手も1本指を折ります。すると、立っている指は左手4本、右手4本なので合計して4+4=8。これが答えの十の位。
次に、両手の折っている指の数同士をかけます。左手は1本、右手は1本なので1×1=1。これが答えの一の位。この8と1を合わせて9×9は81。
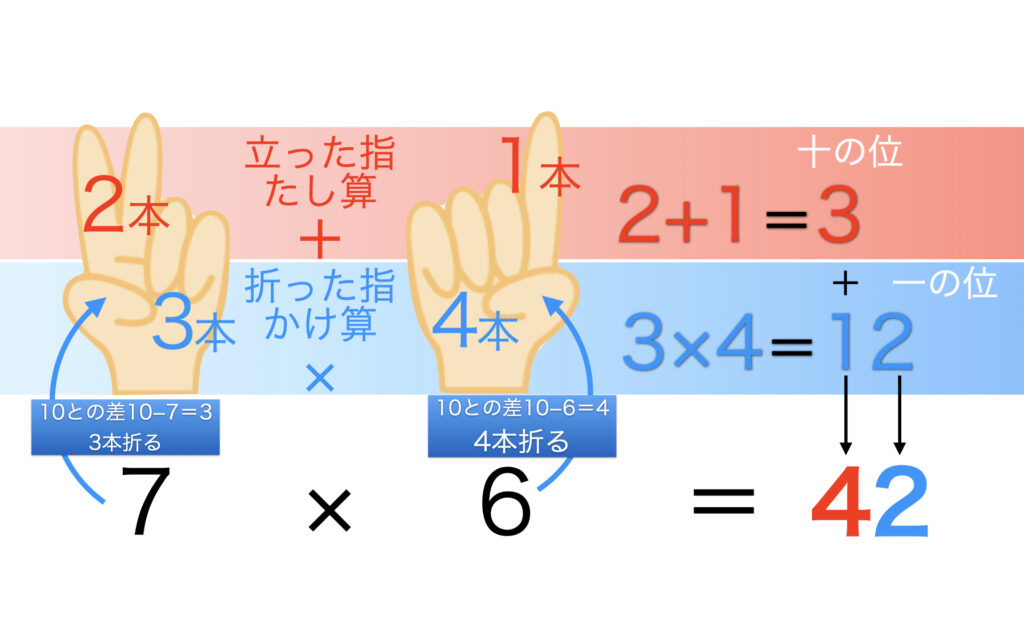
7×6=42の場合
左手は10−7=3、3本指を折ります。右手は10−6=4、4本指を折ります。折った指の数同士をかけて3×4=12。一の位の2は答えの一の位。十の位の1は答えの十の位にたします。立っている指は左手2本、右手1本なので答えの十の位は合計2+1=3、さきほどの1とあわせて答えの十の位を3+1=4とします。4と2を合わせて7×6は42。
なぜ? タネ明かし
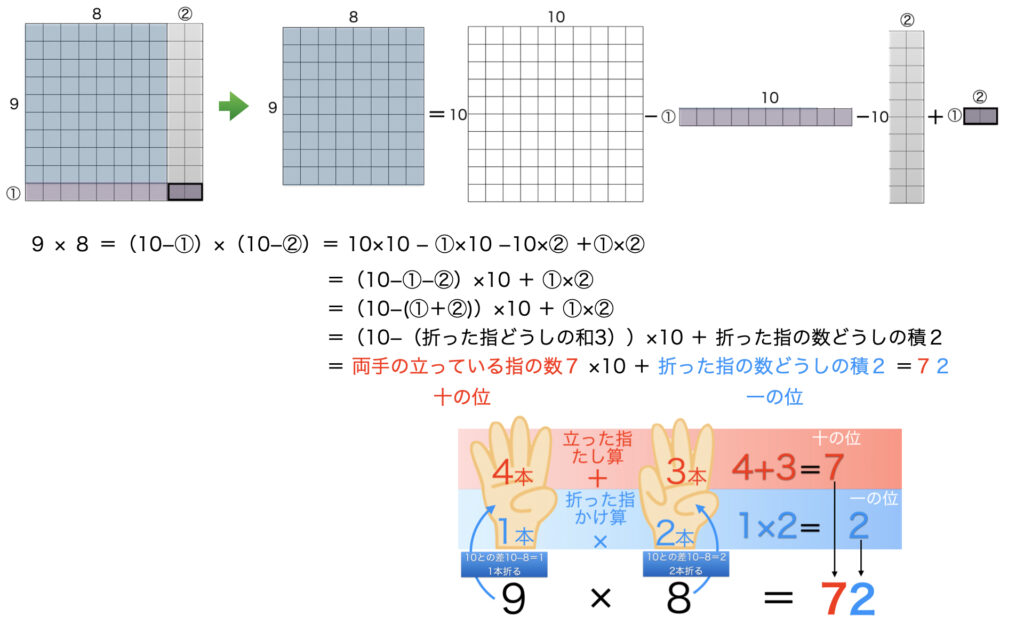
この計算法の仕組みを図を用いて説明してみます。9×8を例にします。まず9×8を次のように変形します。
= 10×10 − ①×10 − 10×② + ①×②
最初の3項は10を共通因数としてくくり出すことができます。
したがって、
すると(10−①−②)は、10本の指から折った数の和①+②=3を引いた数7のことなので、言い換えると「両手の立っている指の合計」です。これが10倍されるからこの数は十の位の数を表します。
そして、最後の①×②=2とは、「折った指の数どうしの積」で答えの一の位です。こうして9×8の答えは、十の位が「両手の立っている指の数」である7と一の位が「折った指の数どうしの積」である2をあわせて72と計算できるわけです。
以上の計算を面積で表すと次の図のようになります。
九九には秘密が隠されている
こうして81通りの九九のうち、5以上×5以上の組合せ5×5=25通り(図の赤囲み内)は残りの56通り(図の橙囲み内)を用いて計算できることがわかります。
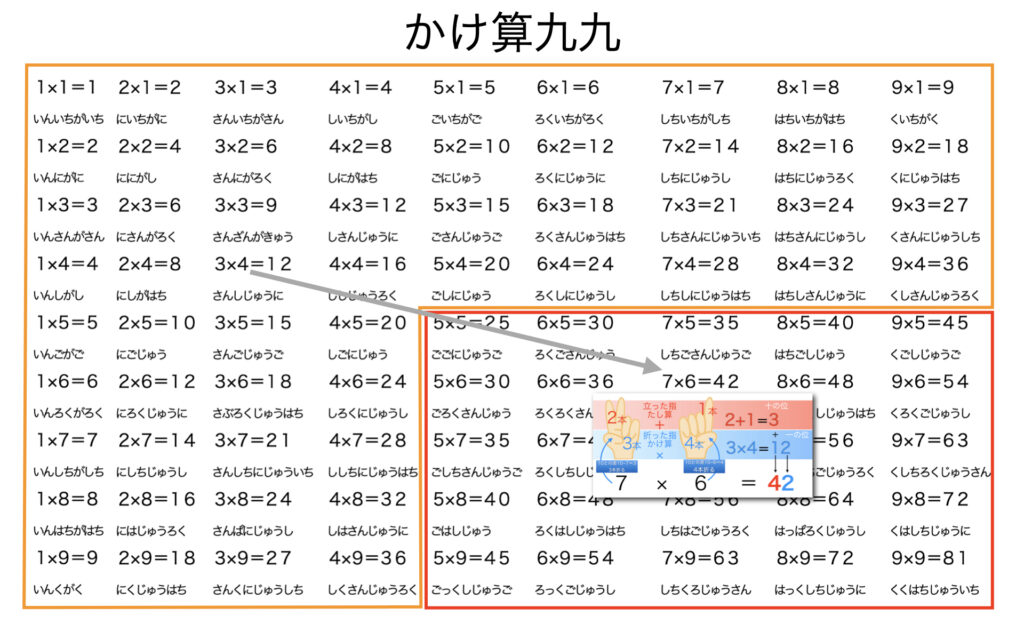
前回の九の段の計算法と今回の計算法で9×8=72(くはしちじゅうに)の計算を並べて眺めてみると両手の中にこんな計算が隠れていたのかと驚かされるでしょう。今回の計算方法は他のかけ算にも応用することができます。その前に、ここで江戸時代の九九を振り返ってみようと思います。次回は「江戸時代の九九は36通りだけ!?」です。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






