謎が多い割り算
四則演算はすべて小学校で習います。中でも割り算と分数には興味深い疑問が満載です。
・そもそも、分数の四則のルールは特別なのか?
・循環小数(1/3=0.333333…、1/7=0.142857 142857 …)のなぞ
・「分数」「有理数」という用語の由来
今回は「0で割る」を取り上げたいと思います。
小学生に「なぜ0で割っていけないの?」「なぜ0で割れないの?」と質問されたらどうこたえるでしょうか。
まちがっても「そう決まっているの!」などと乱暴なレスポンスをしてはいけません。丁寧に答えてあげたいものです。
そもそもこの質問はとても自然で大切な質問です。まずは「いい質問だ!」「おもしろい質問だ!」と褒めてあげます。そして、どこがいい質問で、何がおもしろいのか、解説してあげましょう。
電卓で「3÷0」を計算した結果
電卓で「3÷0」「0÷0」の計算をしてみた結果は次のようになります。
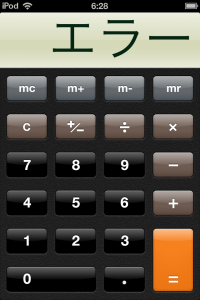

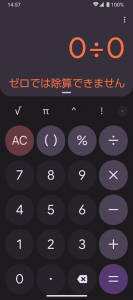

結果は「エラー」「ゼロでは除算できません」「数学的誤りか計算範囲超えです」という3通りの表現でした。
みなさんの電卓でも「3÷0」「0÷0」を計算してどんな表示がされるかを確かめてみましょう。
エラーの意味
例えば、60(km/時)とは60/1(km/時)のことで、1時間で60km進む速さのことです。すると、60/0(km/時)とは0時間で60km進む速さを意味することになりますが、そのような速さは存在しません。
60÷0を電卓で計算した結果「エラー」とは、0で割る計算には答えが存在しないことを表しているようです。
error(エラー)とは、一般には誤り、間違い、誤解、過ちといったことを意味します。数学では、計算の誤差という意味で用いられる場合もあります。
では60÷0=(エラー)は、誤り、間違い、誤解、過ちを意味するのでしょうか。
かけ算で考える
まず割り算とは何かをもう一度考えてみるところから始めてみます。
2×3=6 ↔ 6÷2=3
このように割り算に対応するかけ算を考えることができます。
0で割るわり算「3÷0」に対応するかけ算を考えてみます。
? → 3÷0= ⍰
すると次のようにかけ算の式を考えることができます。
0× ⍰ =3 または ⍰ ×0=3 ← 3÷0= ⍰
割り算の式の ⍰ を考える代わりに、かけ算の式の ⍰ を考えてみるということです。
0× ⍰ =3とは、0に何をかけたら3になるか?ということです。
そんな数はない! そうです、3÷0の答え ⍰ は「ない」です。
しかし、0の割り算はこれで終わりません。0で割るわり算のちょっと面倒なのはこの続きです。
0÷0は特別
0を0で割るわり算です。同じようにかけ算の式を探してみます。
? ← 0÷0= ⍰
すると、次のようになります。
0× ⍰ =0 または ⍰ ×0=0 ← 0÷0= ⍰
かけ算の式の⍰に当てはまる数を考えます。おもしろいことに⍰に当てはまる数はいくらでも見つかります。
0×0=0 → 0÷0=0
0×1=0 → 0÷0=1
0×2=0 → 0÷0=2
0×3=0 → 0÷0=3
… → …
つまり0÷0の答えは「無数にある!」となります。
0で割れる!
以上から、「どうして0でわっていけないの?」の問い自体が修正を迫られます。
「0で割ることはできない」ではなく「0で割る計算はできる」のです。
「いけない」というのは、許されないというニュアンスです。0で割るわり算はそれ以外のわり算と同じように考える(計算する)ことができる(許される)のです!
答えをまとめてみましょう。
0÷0の場合 0÷0=(すべての数)
a÷0は「割ってはいけない」ではなく「定義できない」
以上が小学校6年生に何とか説明できる解説です。これを大人向けに答えるとどうなるかをつづけましょう。
0で割る割り算以外のわり算は6÷3=2、0÷5=0のように「答えが1つに決まる」という大きな特徴を持っています。もちろん、たし算3+5、ひき算6−4、かけ算8×3もそうです。これに対して「a÷0」は「答えが1つに決まらない」という結果になります。
数学ではこのことをそれぞれ「演算が定義できる」「演算が定義できない」と表現します。
「計算(演算)が定義できる」とは、1+1、3-9、9×5、3÷7のように「答えが一つに定まる」ことをいいます。
a÷0の計算結果
a÷0という計算は、答えが2通りになります。a÷0は、答えが一つに定まらない(存在しない)計算です。これを数学では「計算(演算)が定義されない(できない)」と表現します。これが「0で割ってはいけない」の正体です。
よく言われる「0で割ってはいけない」「0で割ることはできない」という表現は「0で割る計算(演算)は定義できない」と比べると、どちらも「できない」という否定表現のところだけは合っています。
0で割る割り算
aが0の場合は、a÷0は無数に存在する。
したがって、わり算a÷0は定義されない。
このように答えを返してくる電卓があってもいいと思います。7÷0には「存在しない」、0÷0には「すべての数」と返してくる電卓アプリです。

おまけ
電卓をアプリを探してみたら次が見つかりました。ubuntu22.04のアプリ「電卓」では「ゼロ除算は未定義です」と表示されます。これまでに見た電卓の中で最も正確な表現です。
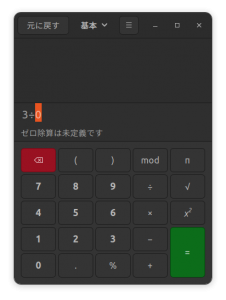
「計算が定義されない」なんて学校の数学にはでてきません。それはそうです、小学校から習う計算のすべては「定義できる計算」だけなのですから。
わざわざ答えが一つに定まらない「定義されない計算」など学校では扱いません。結果として「定義できる計算」だけが安心して教えられます。
ということは、計算(演算)は、定義できるかできないかが確かめられていることでもあります。
分数の四則のルールはなぜそれぞれあのように決まっているのでしょうか。実は四則すべてがきちんと「定義された」計算なのです。
だから安心して分数の計算ができます。本当はいちいち説明できるのですが、残念ながら学校でそこまでふみこむことは容易ではありません。高校数学でもそのことには触れられません。
小学校で習う計算に「なぜ」「どうして」という疑問の眼差しを向けることで教科書には書かれていない風景に出会うことができます。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





