
フィボナッチ数たし算マジック その1
1と1からはじめてたし算することでつくられていくフィボナッチ数は見た目は簡単です。簡単こそ奥深いのが数学です。フィボナッチ数の面白い性質をマジックを通してみていきます。
フィボナッチ数が書かれた表を準備します。相手に次のように問いかけていきます。
私:フィボナッチ数F₁からF₁₀の中からどれか1つえらんでください。
あなた:F₇
私:では、F₁からF₇までのフィボナッチ数の合計はいくつ?
あなた:えーと、1+1+2+3+5+8+13だから…
私:答えは33!
あなた:どうしてそんなにすぐにわかるの!
もう一回
私:フィボナッチ数F₁からF₁₀の中からどれか1つえらんでください。
あなた:F₅
私:では、F₁からF₅までのフィボナッチ数の合計はいくつ?
あなた:えーと、1+1+2+3+5だから…
私:答えは12!
あなた:どうしてそんなにすぐにわかるの!
という具合です。F₁から相手が選んだフィボナッチ数までの合計を一瞬で当ててみせるたし算マジックです。
タネ明かし「2つあとから1を引く」
フィボナッチ数たし算マジックのタネ明かしはこうです。フィボナッチ数の1番目からn番目までのn個の和は、n+2番目のフィボナッチ数から1を引いた数です。
7番目までの和なら、9番目のフィボナッチ数F9=34から1を引いた値。つまり、34-1=33。18番目までの和なら、20番目のフィボナッチ数F20=6765から1を引いた値。つまり、6765-1=6764。
最初の表はF₁₂まで用意して、問題では2つ手前のF₁₀までの中から選んでくださいと問題を出します。F₂₀までの表なら、2つ手前のF₁₈まで、というように表の一番大きなフィボナッチ数の2つ手前までの中から選んでもらうようにします。

フィボナッチ数たし算マジック その2
次の図のような表を用意します。表はあった方が数字を書きやすいですが、なくてもできます。
私:すきな数を2つ、縦に書いてください。
あなた:2と4
私:それを1番目、2番目の数としてフィボナッチ数の時のように順にたし算をして10番目の数までの合計はいくつになるでしょうか。
あなた:3番目は2+4=6、4番目は4+6=10、5番目は6+10=16、6番目は10+16=26、7番目は16+26=42、
私:10番目までの合計は462です!
あなた:どうしてそんなにすぐにわかるの!
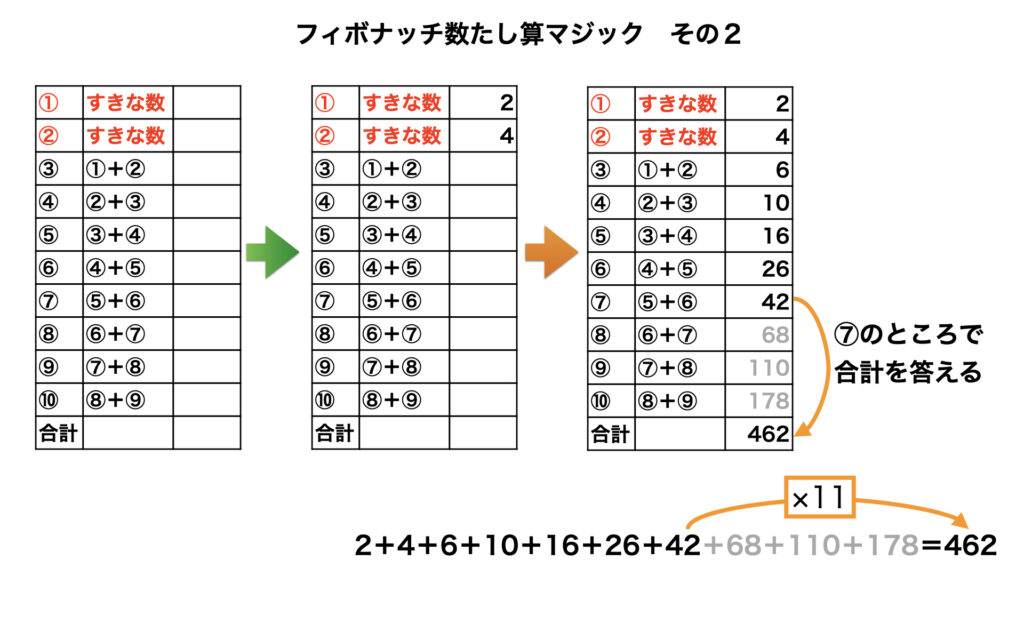
という具合に、相手が自由に選んだ2つの数からはじめてフィボナッチ数と同じたし算をして10番目までの合計を考えさせる問題です。7番目がわかったところで合計を答えてあげることで相手はビックリ、というマジックです。
はじめの2つの数が5と6であれば次のようになります。7番目が73とわかったところで、10個の数の合計は803とわかります。
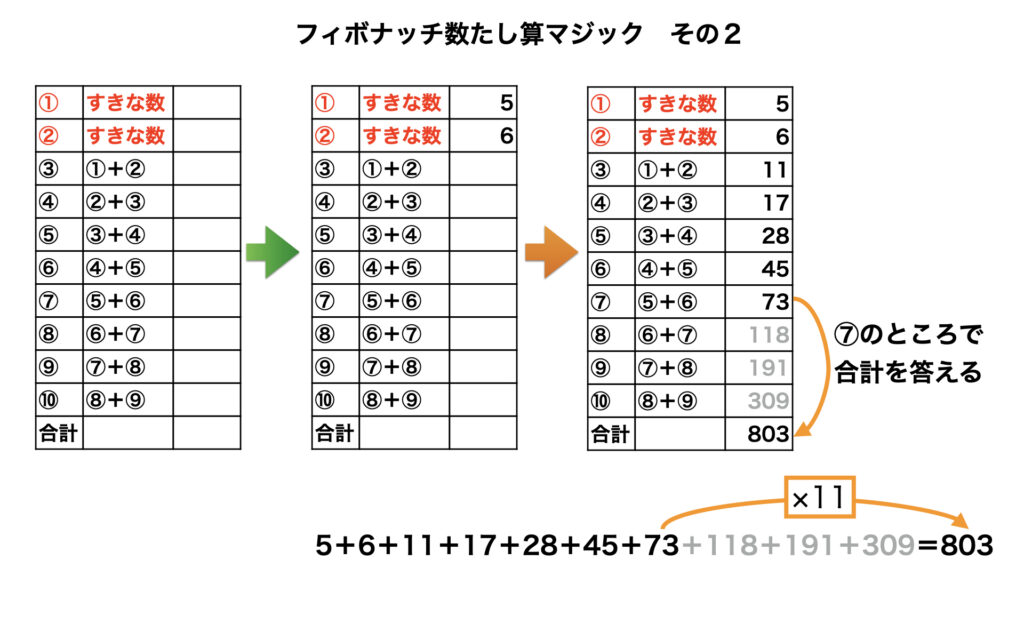
タネ明かし「7番目の数に11をかける」
7番目の数に11をかけた数が10個の数の和になります。2と4からはじめた場合、7番目が42なので、42×11=462とわかります。5と6からはじめた場合、7番目が73なので、73×11=803とわかります。
たしかに、それぞれ
と合っています。
11のかけ算マジック
タネ明かしが「7番目の数に11をかける」のポイントは11のかけ算です。これにもマジックがあります。13×11であれば、1と3の間に1+3=4を挟み込めばいいのです。
59×11であれば、5と9の間に5+9=14の一の位4を挟みこみ、十の位1は答えの百の位にくりあがります。
59×11 → 5□9 → 5+9=14の4を□にいれて、1をくりあげる→ 649
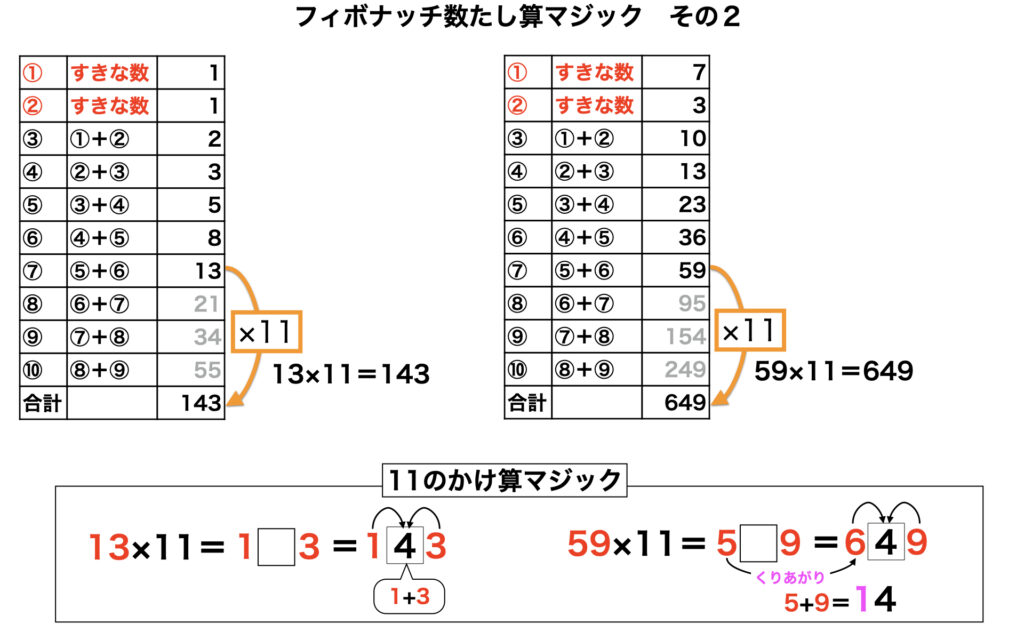
こうして、フィボナッチ数たし算マジックその2は「11のかけ算マジック」をマスターしておけば素早く答えを出すことができます。
フィボナッチ数たし算マジックその1 「7番目の数に11をかける」の謎解き
タネ明かしがわかればマジックはできます。でもどうしてそうなるかはわかりません。タネ明かしの謎解きをしてみましょう。
フィボナッチ数は、1と1から初めて2つの数を足し算してつくられていきます。
これらたし算の式を次のようにひき算の式に変えてみます。
すると、F₁からF₇まで和1+1+2+3+5+8+13は次のように計算できます。
2と-2、3と-3、5と-5というように和が0になる組合せが次々とあらわれるので差引
となります。最後に残る34-1とはF₉-F₂のことです。
同じようにしてF₁からF₂₀までの和を計算してみると、やはり和が0である組合せが次々とあらわれて、最後に残るのが17711-1=F₂₂-F₂となります。
フィボナッチ数の1番目からn番目までたし算するフィボナッチ数たし算マジックは、n+2番目のフィボナッチ数からF₂すなわち1を引いた数が求める和になるということです。

フィボナッチ数たし算マジックその2「①から⑩までの和=⑦×11」の謎解き
フィボナッチ数たし算マジックその2のタネ明かしは
はじめに選んでもらう2つの数を①=aと②=bとおいてみます。すると、③=a+b、④=②+③=a+2b、⑤=③+④=2a+3bというように計算できます。⑩=21a+34bとなるので、①から⑩までの和は55a+88bとわかります。
さて、⑦=5a+8bと①から⑩までの和は55a+88bに注目してみると
実は、7番目まで計算しなくても、はじめの2つのaとbがわかれば、
計算に自信がある人はこの方法で答えを出すこともできます。

執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





