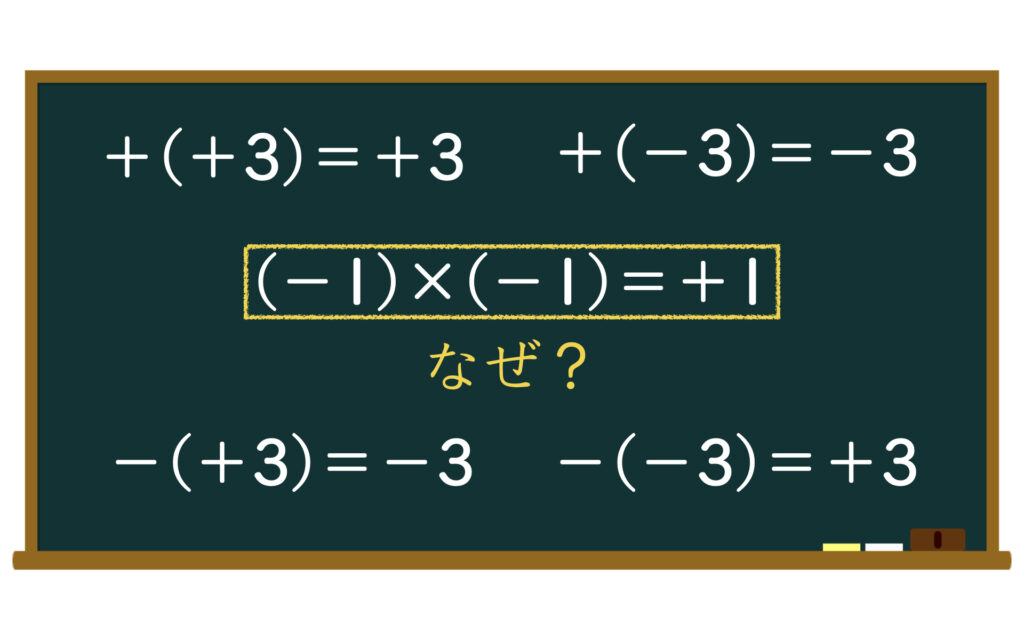
中学で覚えた(−)×(−)=(+)
今も昔も負の数は中学数学で学びます。負の数自体を納得することは容易です。ところが、×(−)という演算となるとそうはいきません。結局、公式として覚えてしまうことになります。
(+)×(+)=(+)
(+)×(−)=(−)
(−)×(+)=(−)
(−)×(−)=(+)
数学の学びにおいてすべてを「理解」することは容易ではありません。「信じる」「覚える」ことで数学を使う・計算することができるようになります。経験を重ねることで「理解」「納得」を得られるようになります。
今こそ中学で覚えた(−)×(−)=(+)を納得する時です。
プラスとマイナスの数
まずは数の正と負の意味からはじめていきましょう。0という基準があって0よりも大きい数を正の数、小さい数を負の数と決めることは誰もが納得するところです。
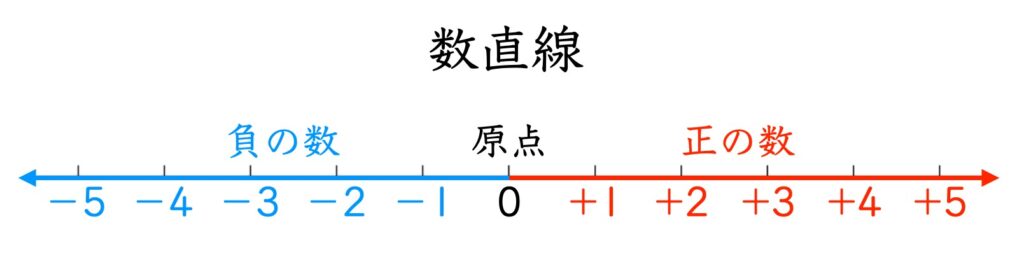
数は正か0か負のどれかです。数直線という図形を用意して、0の位置を決めるとその左側が負、右側が正です。身近な例では温度です。0度に対して大きい温度がプラスの温度、小さい温度がマイナスの温度でマイナス10度(氷点下10度)などと使われます。

正負の数の足し算と引き算から分かること
正負の数の足し算と引き算を数直線を使って考えてみます。7−3=4は(+7)+(−3)と考えて、「0から右に7だけ進み、次にそこから左に3進むと+4のところに行き着く」と考えることができます。
−5+3なら(−5)+(+3)と考えて、「0から左に5だけ進み、次にそこから右に3進むと−2のところに行き着く」という具合です。数直線上において−5という数は原点から左向きに5だけ離れた点、+3という数は原点から右向きに3だけ離れた点を表すといえます。正負というのは「向き」を表していることがわかります。
(−1)を掛けると向きが反対になる
かけ算では「向き」の考え方がポイントになります。
例1.(+3)×(+2)=+6
(+3)×2×(+1)と考えます。はじめの(+3)×2は(+3)+(+3)のことですから(+6)になります。それに(+1)を掛けるとはその+6の向きを同じ向きにすること、つまりそのままの+6が答えとなります。
例2.(+3)×(−2)=−6
(+3)×2×(−1)と考えます。まず、(+3)×2=+6それに(−1)を掛けるとはその(+6)の向きを反対向きにすること、つまり−6が答えとなります。つまり「(−1)を掛けると向きが反対になる」ということ。
例3. (−3)×(−2)=+6
(−3)×2×(−1)と考えます。(−3)×2=(−3)+(−3)=(−6)これに−1を掛けるとその向きを反対にするので+6になります。
そもそも−3とは、右に3進む(+3)ことに対して、逆に左に3進むことを表します。(−3)=(+3)×(−1)の×(−1)には逆向きに進ませる働きがあるということです。
(−1)×(−1)=1 論理的整合性その1
数学の世界は整合性(論理的整合性)があるようにできています。あるところで成り立つことは別なところでも成り立たなければなりません。数と計算の世界には、次のような基本的なルールがあります。
〔1のルール〕1×a=a、a×1=a
〔0のルール〕0×a=0、a×0=0、a+(−a)=0、−a+a=0
〔分配法則〕a×(b+c)=a×b+a×c
これらのルールと(−)×(−)=(+)に整合性があることを確認してみます。
〔0のルール〕から
1+(−1)=0
この両辺に(−1)をかける
(−1)×(1+(−1))=(−1)×0
左辺は〔分配法則〕、右辺は〔0のルール〕により
(−1)×1+(−1)×(−1)=0
〔1のルール〕から(−1)×1=−1なので
−1+(−1)×(−1)=0
すると〔0のルール〕から
(−1)×(−1)=1
(−1)×(−1)=1 論理的整合性その2
第18回:関数電卓って何に使うの?と第19回:関数電卓でπ!?で三角比・三角関数を関数電卓で計算する方法を紹介しました。
その三角関数と(−1)×(−1)=1に整合性があることを確認してみます。ポイントは2倍角の公式です。
2倍角の公式 cos²θ=(1+cos2θ)/2
(−1)×(−1)= cos180º×cos180º
= cos²180º
= (1+cos 2×180º)/2
= (1+cos 360º)/2
= (1+1)/2
= 1
(−1)×(−1)=1 論理的整合性その3
虚数iはi²=−1という性質をもつ数です。虚数は三角関数と深く結びついています。次はその代表的な公式です。虚数と三角関数と(−1)×(−1)=1に整合性があることを確認してみます。
ド・モアブルの公式 (cos x+i sin x)n = cos nx+i sin nx (nは整数)
−1= cos180º= cosπ=cosπ+i sinπ
であるから
(−1)×(−1)=(−1)²
=(cosπ+i sinπ)²
= cos 2π+i sin 2π
= 1+i×0
= 1
まだある(−1)×(−1)=1と〇〇の整合性
×(−1)は向きを変える、(−1)×(−1)=1と分配法則、(−1)×(−1)=1と三角関数、(−1)×(−1)=1と虚数、というように負の数のかけ算は数学の中に整合性を持つことを紹介しました。
数学の世界はうまくできている、ということです。覚える数学はけっしてネガティブではありません。覚えることでとにかく数学を使ってみる・数学に触れてみることができます。そのうちに納得する数学にチャレンジしてみようという気持ちになります。
今回紹介したものとは別の数学から(−1)×(−1)=1を導くことで、中学数学で覚えた(−1)×(−1)=1を納得する(−1)×(−1)=1に変身させてみましょう。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





