
関数電卓には「π」がついています。このボタンを押せばπは表示されますがこれでは面白くありません。何か数式を入力して、つまり何かを計算してその答えがπになるような数式を考えてみます。
理屈は後回し。まずは答えの数式を入力してπが出ることを確かめてみるところからはじめます。
関数電卓の準備 RADモードに切り替える
関数電卓にはRADモードとDEGモードという2つのモードがあります。まずRADモードに切り替えます。アンドロイドOSの電卓アプリでは、ボタン左側にある「RAD」「DEG」のボタンを使います。「RAD」のボタンを押すとRADモードになりボタンは「DEG」の表示になります。
電卓アプリを起動して「DEG」であればOK、「RAD」であればこれを押して「DEG」の表示に切り替えます。これで準備OK。
答え「4×tan-1(1) 」を入力
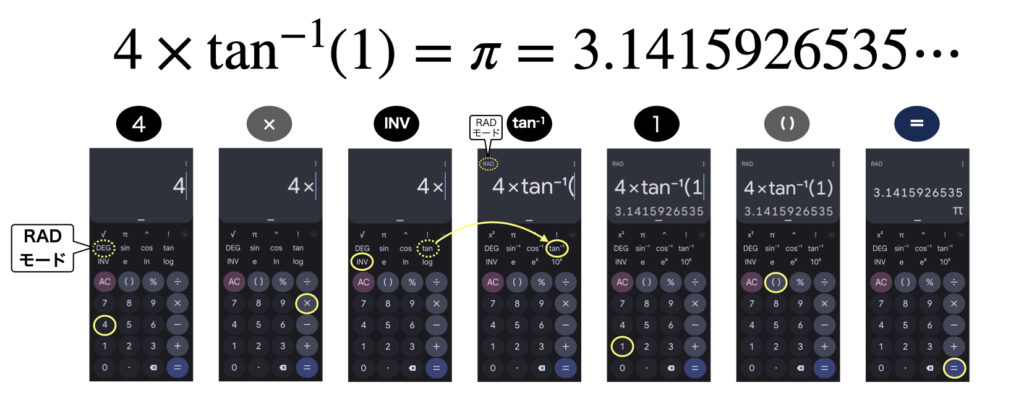
つぎの図の手順でボタンを押していってみよう。はたして、関数電卓には3.1415926535とπが表示されるはずです。「INV」を押して「tan」のボタンが「tan-1」に変えるところがポイントです。
三角比とは何か
なぜ「4×tan-1(1) 」がπを表す式なのかを説明していきます。前回「関数電卓って何に使うの?」では、三角比tan(タンジェント)だけを紹介しました。
あらためて三角比を説明します。三角は三角形のことです。三角定規で説明するのが分かりやすいでしょう。2種類の三角定規はどちらも直角三角形です。1つは内角が30°、60°、90°の“鋭角三角形”、もう一つは内角が45°、45°、90°の“直角二等辺三角形”です。
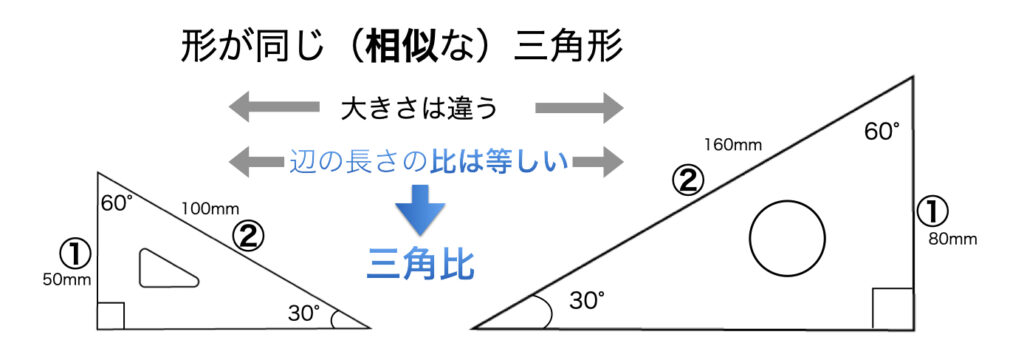
2つの大きさが異なる三角定規──“鋭角三角形”を比べてみます。2つの三角形は大きさは違うけれど同じ形です。拡大・縮小して重なる2つの図形は相似であるといいます。
相似な三角形は対応する角が等しく、対応する辺の比が等しくなります。2つの相似な三角形の斜辺と高さの比はどちらも2:1です。これが「sin30°=1/2」という三角比です。どちらの三角形でも「sin30°=1/2」です。三角比は三角形の大きさではなく角度で決まる値です。
3辺のうち2辺の取り方で3通りの比を考えることができます。sinは高さ:斜辺、cosは斜辺:底辺、そしてtanは高さ:底辺という組合せです。
もう一つの角度の単位「RAD」
角度を分度器で測るのが「DEG」(単位「°」)であるのに対して、角度を定規で測るのが「RAD」です。
半径1[m]の円を考えます。直径が2[m]だから円周はその円周率π倍すなわち2×π[m](約6.28[m])です。すると、360°に対して円周2π[m]を対応させることができます。これが定規で角度を測るという意味です。
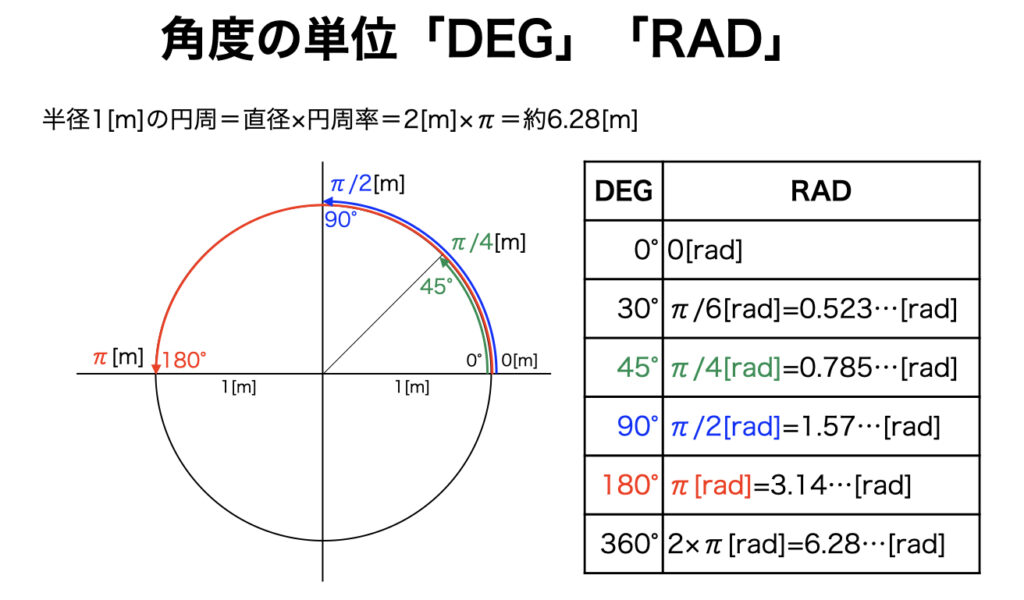
角度であることを表すための単位がrad(ラディアン)です。[m]を[rad]に置き換えます。360°は2×π[rad]、180°はπ[rad]のように表します。π/2[rad]は90°を表すことになります。ちなみに「DEG」は度数法、「RAD」は弧度法と呼ばれます。
関数電卓で三角比を計算
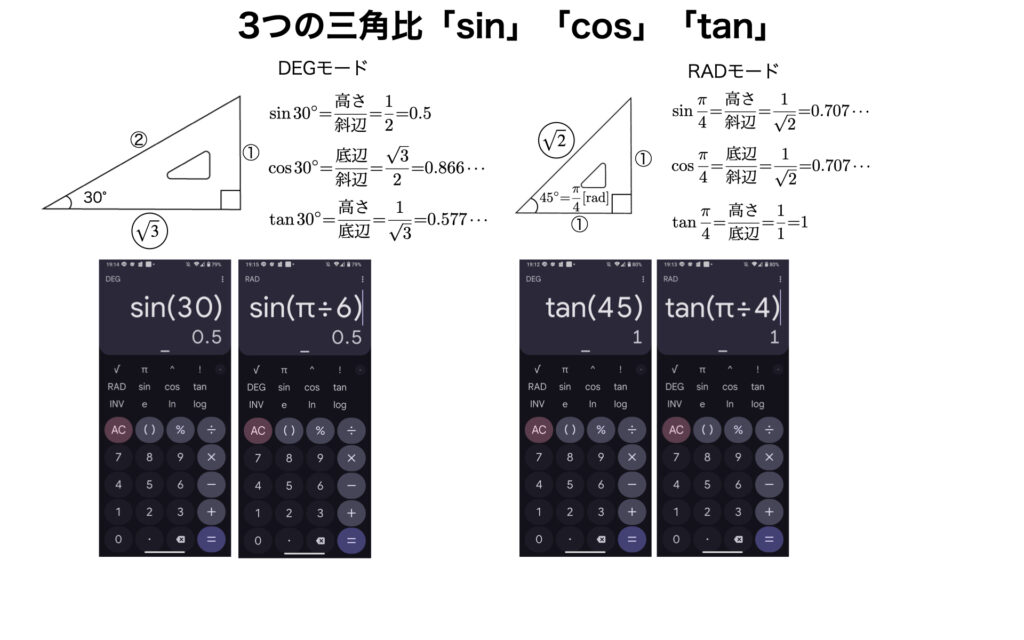
DEGモード、RADモードで同じ角度の三角比が同じになることを確かめてみましょう。sin30°とsin π/6がどちらも0.5になります。tan45°とtan π/4がどちらも1になります。
tan-1を理解する
論より証拠。つぎの関係を眺めてみてください。sin、cos、tanに慣れてきたならば、sin-1、cos-1、tan-1もあっという間です。
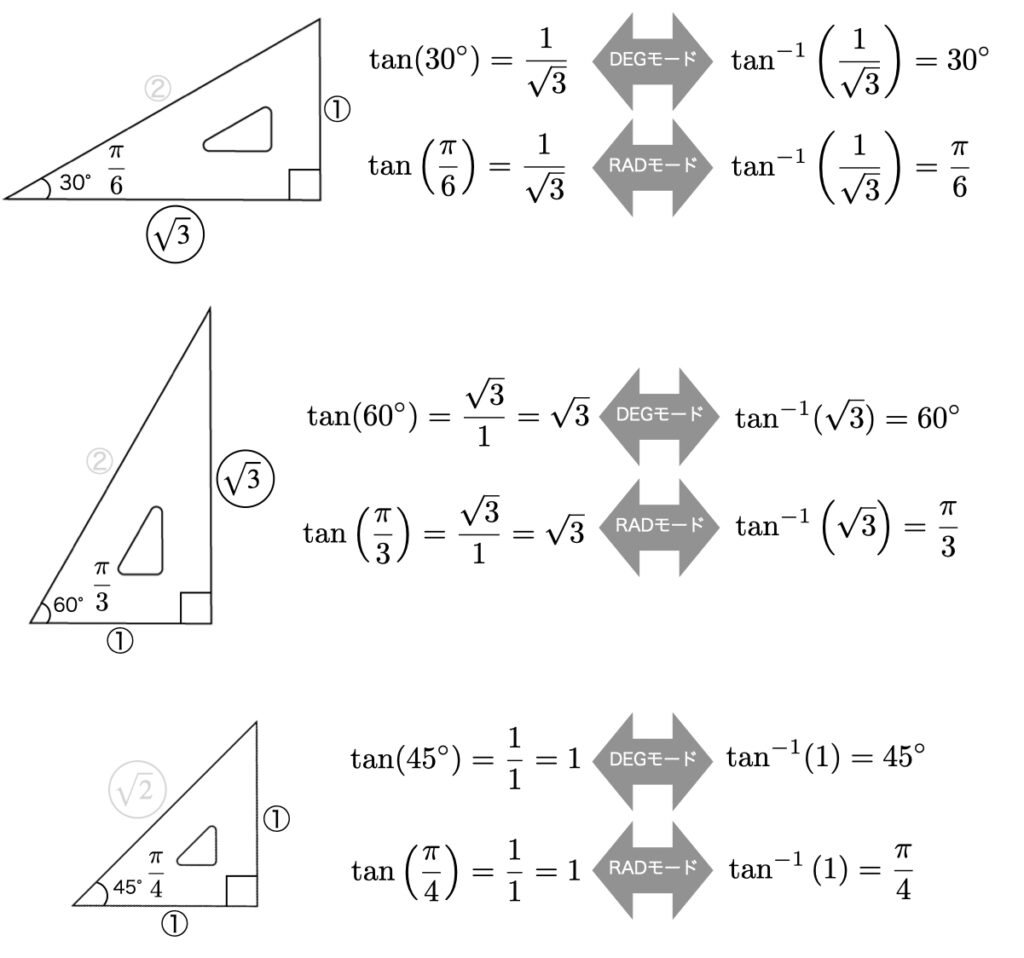
角度とtanの値を入れ替えたものがtan-1の式になるということです。三角比 sinθ、cosθ、tanθとは角度θに対して2辺の比が分かるものです。それに対して、sin-1x、cos-1x、tan-1xとは、2辺の比xに対して角度が分かるものだということです。
問題の答え
RADモードの3つのtan-1の式に注目してみます。tan-1の値がπ/6、π/3、π/4なので
tan-1の値それぞれを6倍、3倍、4倍したものがどれもπになります。

同じくRADモードのsin-1の式に注目したのが次の答えです。
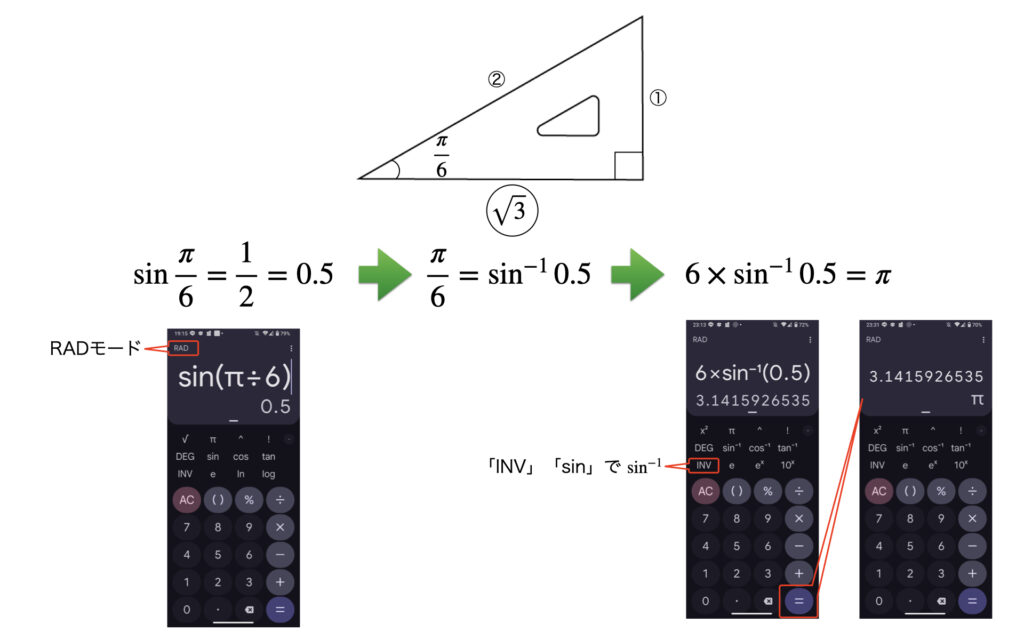
このように三角比sin、cos、tanとsin-1、cos-1、tan-1をRADモードで計算することでπが答えになる数式がつくれるということです。

マチンの公式を関数電卓で計算
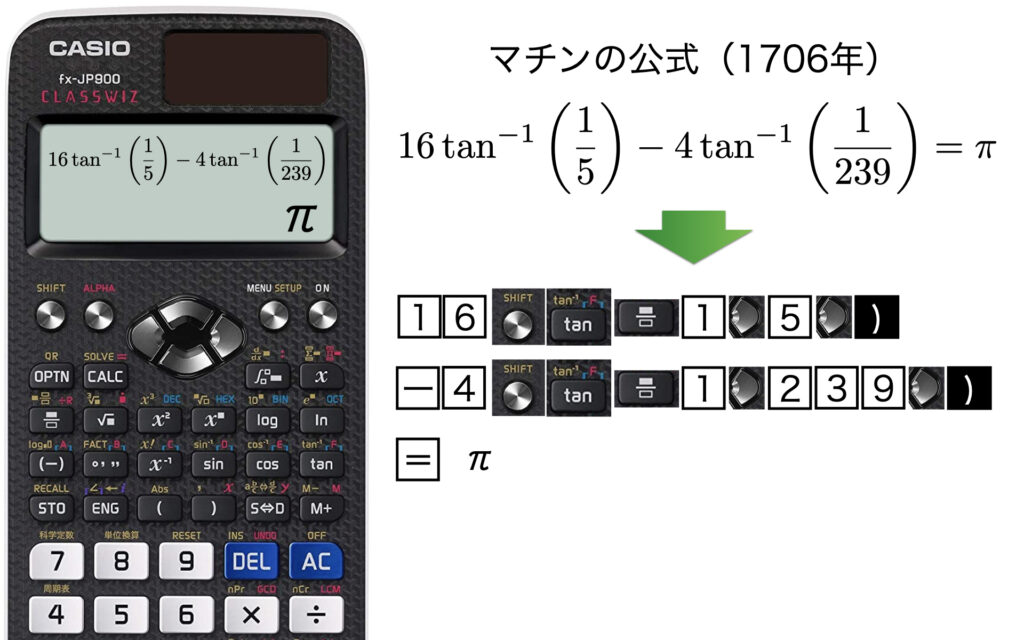
最後に本格的な円周率πを計算する公式を関数電卓で計算してみます。1706年にイギリスの天文学者・数学者ジョン・マチンによって発見されたのがマチンの公式です。tan-1を使っています。
マチンはこの公式を用いて円周率πを100桁(当時の世界記録)求めることに成功しています。CASIOの関数電卓fx-JP900で計算してみると見事にπと表示されました。
次回は満を持して「マイナス×マイナスはなぜプラスになる?」です。謎解きには三角比も登場します。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





