前回はその1「コピー用紙」、その2「日本建築の曲尺」、その3「偏差値」の中に√が隠れていることを紹介しました。さらに√の計算を探っていきます。

√の計算その4 カーナビ
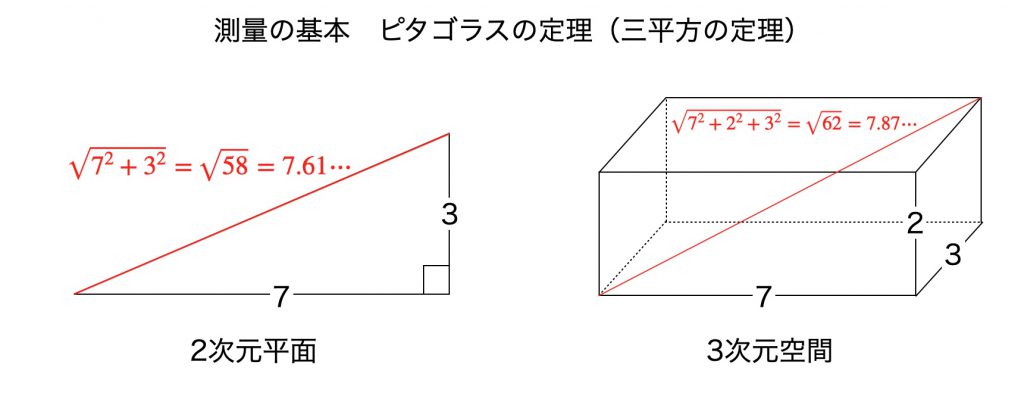
√の計算といえばピタゴラスの定理(三平方の定理)です。ピタゴラスの定理があれば長方形の縦と横の長さから対角線の長さが計算できます。立体の場合には、直方体の対角線の長さが計算できます。
地図をはじめ地球上で自分の位置を精確に確認する測位ための様々な方法が考えだされてきました。最新のGPS衛星を使った測位計算の基本も三平方の定理です。2次元平面、3次元空間における測量の基本がピタゴラスの定理です。
2点間の距離の計算に√が使われるので、距離にまつわる計算には頻繁に√が登場します。その筆頭が地図です。カーナビ(カーナビゲーションシステム)は地上の車の位置をおしえてくれる便利なマシンです。その仕組みは4つ以上のGPS(Global Positioning System、全地球測位システム)衛星からの電波を受信することで、電波が届くまでの時間から距離を計算します。
光速をc(約30万km/秒)としてGPS衛星から受信機(カーナビ)に電波が届くまでの時間をtとすれば、GPSと受信機の距離はctと表されます。GPS衛星の位置を(X, Y, Z)、受信機の位置を(x, y, z)とすると、三平方の定理より
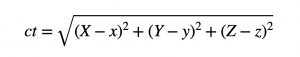
√の計算その5 4次元空間の距離
GPSに使われた√の計算は3次元空間に対するものでした。三平方の定理は4次元空間の2点間の距離の計算にも使われます。【連載|AI時代を生き抜く新しい数学力】第5回数学のリアリティ 受験“数学”でない数学(Math)の力の中で、4次元ベクトルのなす角がわかる!を紹介しました。
人間の目で見ることができるのは3次元空間までです。4次元世界を見ることは不可能です。しかし、数学の目を通すことで4次元いやそれ以上の高次元の世界の様子を知ることができます。以前の連載では、2つの4次元ベクトルx=(2, -1, 3, -2)とy=(-3, 2, 1, 5)のなす角が124.4°になるという結果だけを紹介しました。その途中の計算は次のようになります。
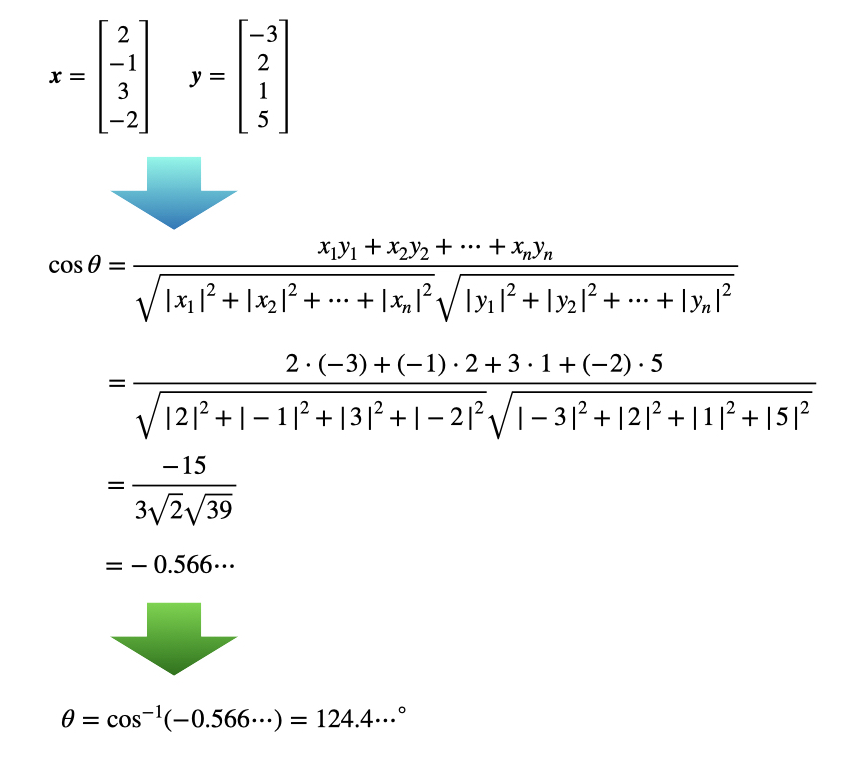
√の計算が確認できます。これは4次元ベクトルの大きさ(長さ)の計算で、三平方の定理の応用です。あらためて前の連載を読んでいただきたいのですが、このような高次元の√を使った計算が、現在のデータサイエンスにも応用されています。2つの日本語のニュースの内容がどれほど近いのか離れているのかがベクトルのなす角で分かります。
√の計算その6 人生の半分(折り返し)は何歳?
次に紹介するのも過去の【連載|人を数学する】第0回人生の折り返しは何歳?からのもので、a歳からb歳までの人生の半分の年齢は√a×bという内容です。
ここでいう時間は感覚時間というものです。時計時間は人間の外で流れる客観的な時間で一定の速さで流れると考えられているものです。それに対して感覚時間とは、人間がその流れを感じている時間のことです。小学1年生の時の1年間と20歳の時のそれは時間の感じ方は違うことを誰もが知っています。
小学1年生の時の1年間の感じ方は大人になってからの1年間よりも圧倒的に長いということです。ぜひ電卓の√キーを使ってaとbにいろいろな年齢を当てはめて人生の折り返しの年齢を計算してみてください。

√の計算その7 エレクトロニクス ラジオの製作
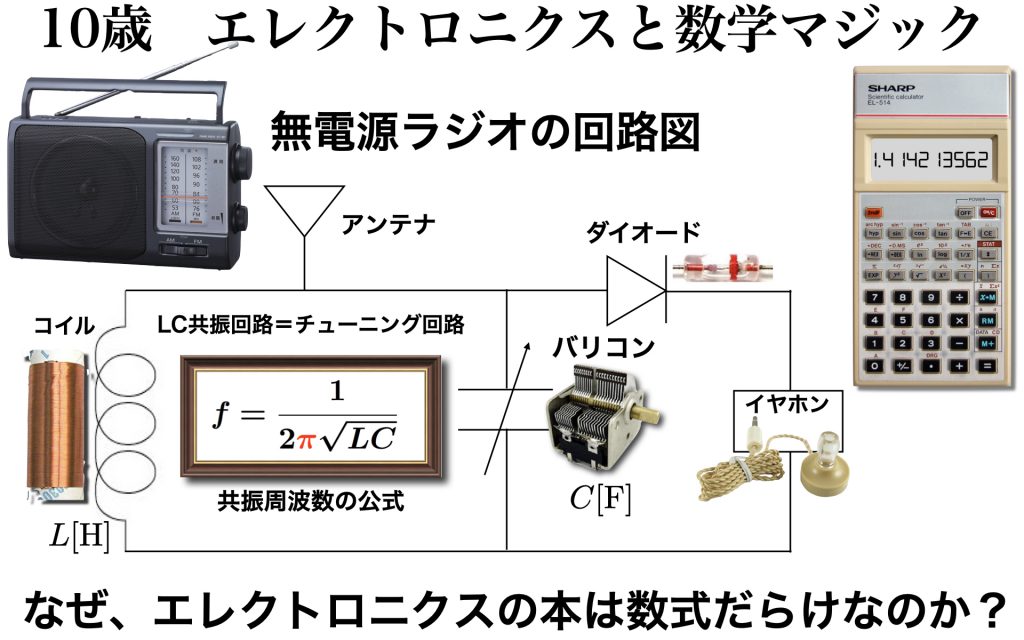
最後は私の√の物語です。ラジオを聴くのが好きだった10歳の時、自分で高性能なラジオを作り始めました。そこで出会ったのが「LC回路の共振周波数の公式」です。Lはコイル、Cはコンデンサーの大きさを表します。ラジオのツマミを回すことでコンデンサーCの大きさが変化します。すると受信周波数も変化します。これがラジオのチューニングの仕組みです。
なぜ公式がこのような姿になるのかはまったく想像できませんでしたが、電卓があれば計算することはできました。公式に当てはめて計算したコイルとコンデンサーを用意して半田ごてを使って回路図通りに配線しラジオを製作していきます。
スイッチを入れてチューニングのツマミを回してみると見事に音楽が流れてきました。そのときの驚きと感動は今も忘れることができません。数学の圧倒的なリアリティを感じた瞬間でした。
目に見えない電気の世界をハンドリングする唯一の方法が数学であることを日々実感していった小学6年生です。「なぜ公式には√とπがあるのか」その疑問を解くまでに6年かかりました。高校2年生で分かったその理屈は想像を超えるものでした。証明に登場したのは三角関数と微分積分と微分方程式という数学。10歳の時以上に、数学の圧倒的な威力に感動しました。
実は「LC回路の共振周波数の公式」の物語はこの後も続くことになり、驚きの展開を見せてくれることになりました。私がサイエンスナビゲーター(R)になることができたきっかけが√の計算だったのです。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





