発生周期が17年のセミ
北米には発生周期が13年ごとと17年ごとに大量発生するセミがいます。13と17は素数なので素数ゼミと呼ばれています。なぜ発生周期が13年、17年なのか、生物学で研究されているのですが、そのポイントは素数であることが明らかになってきました。
素数とは1と自分自身の2つの約数を持つ数のことです。1の約数は1だけ(約数は1個)なので素数ではありません。2は約数が1と2の2つなので素数、3は約数が1と3の2つなので素数です。
4は約数が1、2、4の3つなので素数ではありません。約数の数が3以上の素数ではない数を合成数といいます。したがって、自然数を分類すると、1、素数、合成数の3つのうちどれかになります。
素数ゼミの謎解きの鍵は最小公倍数
素数ゼミの謎解きの鍵は最小公倍数です。最小公倍数について理解を深めるところからはじめます。まずは公倍数について。2と3についてそれぞれの倍数をあげてみると次のようになります。
2の倍数:2,4,6,8,10,12,14,16,18,20,…
3の倍数:3,6,9,12,15,18,21,…
2つの倍数に共通な数がみつかります。これが公倍数です。2と3の公倍数は6,12,18,…です。
すると、この中に最小の6という公倍数があり、これより大きい公倍数は6の倍数であることがわかります。これが最小公倍数です。
ところでこの最小公倍数6は素数2と素数3の積です。素数同士の最小公倍数は素数の積です。5と7の最小公倍数は、2つの素数の積5×7=35です。

そうでない2つの数の場合、最小公倍数はどうなるのでしょうか。どちらも素数2の積で表される数、例えば4(=2×2)と16(=2×2×2×2)ならば、最小公倍数は16です。素数2の個数(2個と4個)の多い方の16が最小公倍数となるということです。
9(=3×3)と27(3×3×3)ならば、素数3の個数(2個と3個)の多い方の27が最小公倍数です。
12(=2×2×3)と18(=2×3×3)の最小公倍数を考えてみます。素数2の個数はそれぞれ2個と1個、素数3の個数はそれぞれ1個と2個です。素数2、素数3の個数が多い方をとって、最小公倍数は素数2が2個、素数3が2個、すなわち2×2×3×3=36となります。
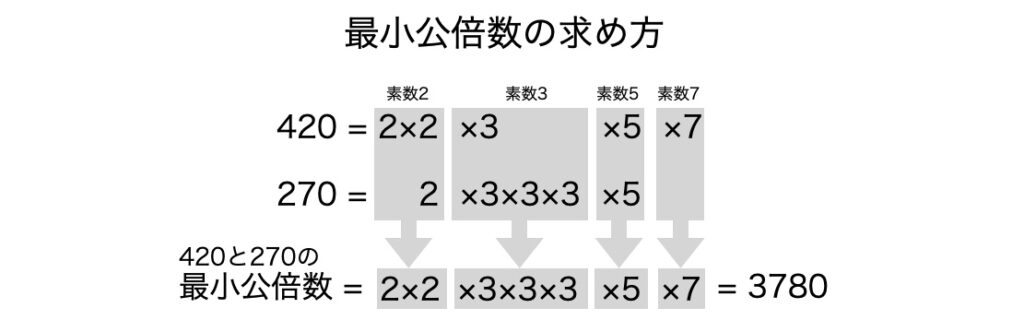
12(=2×2×3)と30(=2×3×5)では、素数2の個数はそれぞれ2個と1個、素数3の個数はそれぞれ1個と1個、そして素数5の個数はそれぞれ0個と1個なので最小公倍数は、素数2については2個、素数3については1個、素数5については1個の積2×2×3×5=60とわかります。
200万年前の氷河時代
これで素数ゼミの謎解きの準備ができました。200万年前の氷河時代、寒さに耐えかねたセミたちは地中にもぐって生きるようになりました。寒い氷河時代でもあまり気温が下がらない場所があったのでそこでセミたちは生き残りました。とはいえ気温は低いのでアメリカ北部のセミたちは14〜18年もの長い間地中で過ごすようになりました。
たとえばある年に15年と18年周期のセミがいっしょに地上に出てこどもをつくったとします。15年後に15年ゼミが、18年後に18年ゼミが地上に出てみたら、他の周期のセミが地上にはいないのでこどもをつくる機会は減りにセミの数が減ってしまいます。
さらに、15年ゼミと18年ゼミの間にできたこどもの周期は16年や17年となってしまい周期が乱れてしまいます。結局、90年(15と18の最小公倍数)ごとに繰り返す15年ゼミと18年ゼミの出会いは双方にとって良くない結果を生みだしてしまうことになります。はたして何万年も経てばどちらも絶滅してしまうことになります。違う周期同士のセミたちは、なるだけ地上で出会わない方が生き延びることができるということです。
周期の違うセミはできるだけ出会わない方が生き延びる
いま14年、15年、16年、17年、18年の5種類の周期をもつセミたちがいるとします。これらから2種類のセミ同士が出会う周期すなわち最小公倍数を求めてみます。
素数17と18(=2×3×3)の最小公倍数17×2×3×3=306
素数17と15(=3×5)の最小公倍数17×3×5=255
素数17と16(=2×2×2×2)の最小公倍数17×2×2×2×2=272
15(=3×5)と16(=2×2×2×2)の最小公倍数2×2×2×2×3×5=240
16(=2×2×2×2)と18(=2×3×3)の最小公倍数2×2×2×2×3×3=144
15(=3×5)と18(=2×3×3)の最小公倍数2×3×3×5=90
15年セミと18年セミは90年ごとに出会うのに対して、17年セミと18年セミは306年ごとに出会います。素数が周期の17年ゼミが入ると最小公倍数は大きくなることがわかります。つまり周期が異なるセミと出会いにくいということです。
何万年、何十万年も経てば最小公倍数の小さい周期のセミは減っていき、最小公倍数が大きいセミだけが生き残っていきます。これが17年周期の素数ゼミが今も生き残っている理由です。
最小公倍数が小さい方が頻繁に地上で出会ってたくさんこどもを残せるから生存には有利と思いきや、現実はそれとは逆でした。できるだけ出会わない方が結局生き延びることができるということなのです。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite





