第13回　ドレミファソラシド謎解きの旅　その3　関数電卓を使ったピアノの音階の謎解き（最終回）

ピタゴラス音律の限界

いよいよ連載11回で紹介したピアノの音階の謎解きをします。前回連載12回ではドレミファソラシドを決めるルール、ピタゴラス音律を紹介しました。

ピタゴラスは、「弦の長さを2/3倍」に短くすることでドからソの音がつくれることを発見しました。周波数は3/2倍すなわち1.5倍になります。するとドとソの2音はきれいにまざります。これが和音です。

さて、「弦の長さを2/3倍」のルールで音をつくっていくと1オクターブ離れた音どうしの周波数がぴったり2倍になりません。これがピタゴラス音律の最大の弱点です。紀元前に考え出されて以来、音のつくり方──音律の研究はピタゴラス音律の弱点を克服することを目標になされました。

1636年、画期的な音律が完成

そして、ついに1636年に画期的な音律が完成しました。音階はドレミファソラシドの間に半音をはさむことで12音となるものです。

12音階
ド→①→ド#→②→レ→③→レ#→④→ミ→⑤→ミ#→⑥→ファ→⑦→ソ→⑧→ソ#→⑨→ラ→⑩→ラ#→⑪→シ→⑫→（ド）

画期的な音律は1オクターブどうしの2音の周波数がぴったり2倍になることを基本にします。それには、1音上がることに周波数が2^1/12倍にすればいいことになります。

①から⑫で周波数が2^1/12倍ずつ大きくなれば、2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12×2^1/12＝2^{1/12+1/12+1/12+1/12+1/12+1/12+1/12+1/12+1/12+1/12+1/12+1/12}＝(2^1/12)¹²＝2¹＝2倍となる計算です。

理論上は単純ですがこの2^1/12の計算が困難を極めます。多くの人々の長年に渡る努力の末、17世紀に正確な計算が完了しました。ではその見事な結果を確かめていきます。ここで関数電卓の出番です。

関数電卓で平均律がつくりだす音階を計算

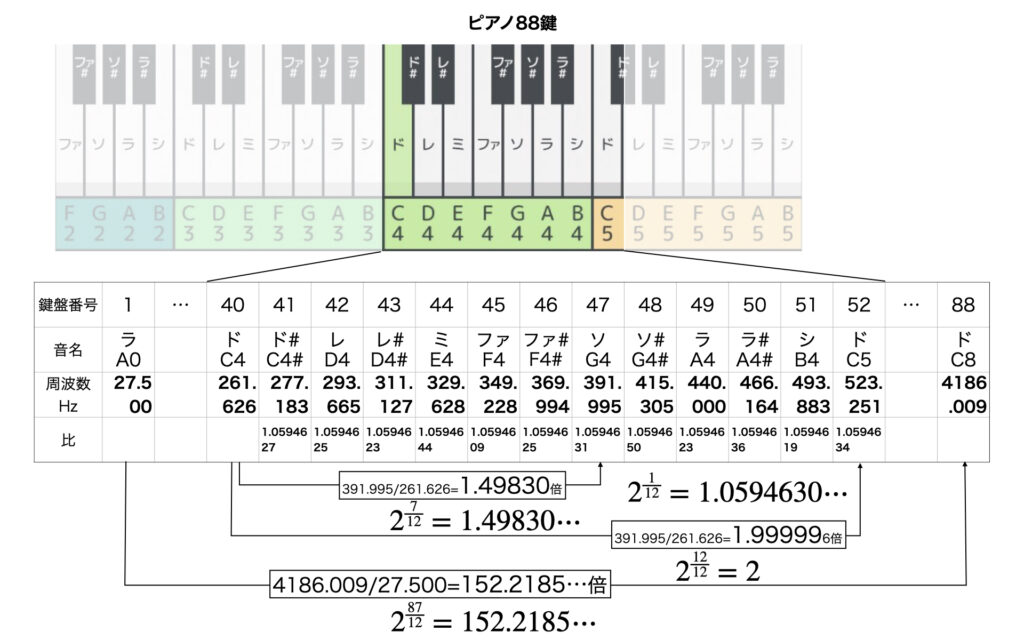
ピアノ88鍵の中から1番目の最低音、88番目の最高音、そして基準音のラ（A4）を含むド（C4）からド（C5）を選んでみます。

そこで、まず隣り合う2音の周波数の比を計算してみます。40番目のドと41番のド#であれば、277.183÷261.626＝1.0594627…という具合です。これを51番目と52番目まですべて計算して表に比の値を記録してみます。

すると12個の比率がすべて1.05946…であることが確かめられます。関数電卓で2^1/12を計算してみます。

「２」「x^y」「(」「１」「÷」「１」「２」「)」「＝」

はたして1.05946309435となります。①から⑫で周波数が正確に2^1/12＝1.05946倍になっていることがわかります。

つぎに、ド（C4）とソ（G4）の2音について周波数の比を計算してみると
391.995/261.626=1.49830
となります。

ド→①→ド#→②→レ→③→レ#→④→ミ→⑤→ミ#→⑥→ファ→⑦→ソだから2^1/12倍が7つあります。つまり、2^{1/12+1/12+1/12+1/12+1/12+1/12+1/12}＝(2^1/12)⁷＝2^7/12となります。これを関数電卓で計算してみると

「２」「x^y」「(」「７」「÷」「１」「２」「)」「＝」

と入力すれば、1.49830707687すなわち1.5に近い値であることがわかります。
この音律ではピタゴラス音律のドとソの関係（ちょうど1.5倍）も小さいズレで実現しているということです。

最後に、1番目の最低音（A０）と88番目の最高音（C８）の周波数の比を計算してみます。4186.009/27.500=152.2185…倍です。さて、1番目から88番目の間には2^1/12が88−1だから87個あります。したがって、2^{1/12+1/12+1/12+1/12+…+1/12+1/12+1/12}＝(2^1/12)⁸⁷＝2^87/12となります。

これを関数電卓で計算してみると


「２」「x^y」「(」「８」「７」「÷」「１」「２」「)」「＝」

と入力すれば、152.218510720すなわち152.2185までぴったり合っています。

12平均律を完成させた数学者マラン・メルセンヌ

この音律の計算を完成させたがフランスの数学者マラン・メルセンヌ（1588-1648）です。有名なメルセンヌ素数2ⁿ-1のメルセンヌ、その人です。数学者メルセンヌは関数電卓ができるはるか昔に2^1/12の計算を完璧に行い音律を完成させました。

この音律は12平均律と呼ばれています。現代のピアノが奏でる美しい音楽は、ピタゴラスやメルセンヌといった数学者たちの計算に支えられているということです。3回にわたるドレミファソラシドの謎解きはこれで終わりです。

執筆者プロフィール

桜井 進（さくらい すすむ）

1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する！数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite