
9□×9◯の計算法 ポイントは100との差

100に近い数同士のかけ算は暗算でできます。ポイントは100との差。98と97のかけ算であれば、100との差はそれぞれ2と3。かけ算の答えを上2桁(百以上の位)と下2桁に分けて計算します。
ステップ1 98と97、それぞれ100との差を求める。98は2、97は3。
ステップ2 2と3の和を計算。100からその和を引いた値が答えの上2桁(百以上の位)。100-5=95。
ステップ3 2と3の積が答えの下2桁(十の位以下)。2×3=6のように1桁になる場合には06とする。
ステップ4 ステップ2の95とステップ3の06をまとめた9506が答え。
99×99であれば、100との差が1。1+1=2、100−2=98。1×1=1だから、答えは2つの数97と02を合わせて9801です。
10□×10◯の計算法 ポイントは100との差
この100に近い数同士の計算法は102×103のように100を超えた数の場合でも適用できます。ただし、9□×9◯の場合と異なるのがステップ2の部分です。
ステップ1 102と103、それぞれ100との差を求める。102は2、103は3。
ステップ2 2と3の和を計算。100にその和を足した値が答えの百以上の位。100+5=105。
ステップ3 2と3の積が答えの下2桁(十の位以下)。2×3=6のように1桁になる場合には06とする。
ステップ4 ステップ2の105とステップ3の06をまとめた10506が答え。
106×107であれば、100との差が6と7。6+7=13、100+13=113。6×7=42だから、答えは2つの数113と42を合わせて11342です。

計算法の謎解き
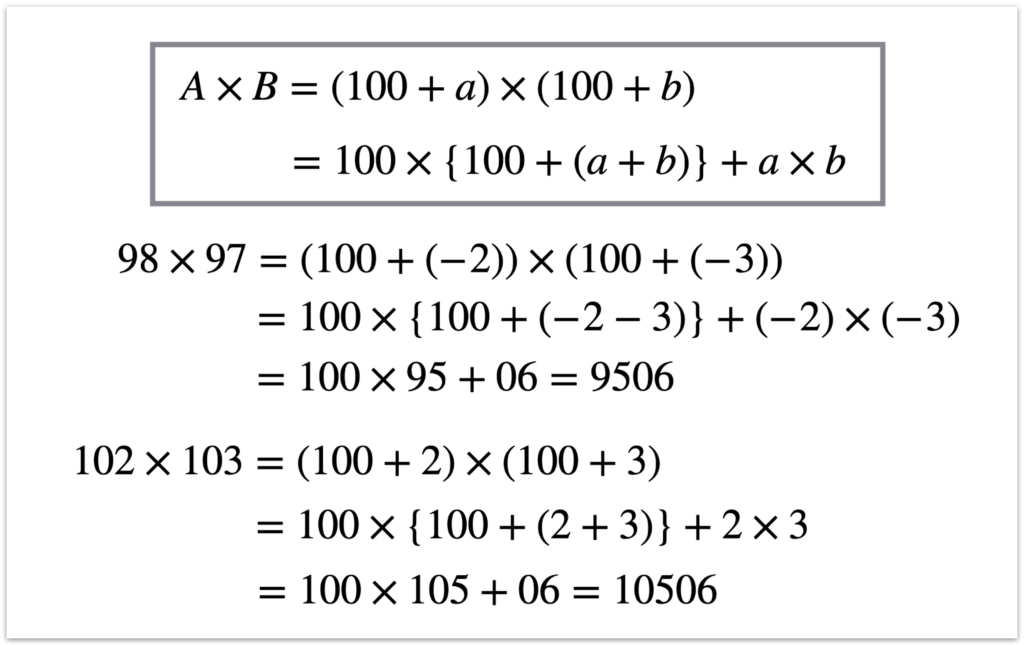
A、Bをそれぞれ100+a、100+bとすれば、A×Bは
A×B=(100+a)×(100+b)
=100×{100+(a+b)}+a×b
=100×{百以上の位}+(十以下の位)
と計算できます。
これより、98×97の場合はaとbがそれぞれ-2と-3と負の値になることからステップ2で100から2+3を「引く」ことになり、102×103の場合はaとbは+2と+3と正の値になることからステップ2で2+3を「足す」となることがわかります。
さらに、98×97をたて×よこ、すなわち長方形の面積と解釈すれば、100×100の正方形から2つの長方形を除くことを考えて、その値を計算することができます。この場合、2つの長方形(100×3と2×100)が交わる小さい長方形2×3が2つ分引かれることになるので1つ分を足すことに注意します。

執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。「桜井進の魔法の算数教室」と「桜井進の数学浪漫紀行」を毎月開催。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite






