ラジオが導いた数学の世界
前回、私が10歳のときにラジオの製作に夢中になり、数学と出会ったことを紹介しました。数学の圧倒的なリアリティを実感できたことは私にとって生涯を通しての財産となっています。
今回はこの出会いについて別な視点から分析してみようと思います。10歳の私にとって、共振周波数の公式は未知だらけの存在でした。しかし、諦めることなく公式と向かい合ったのは、それがチューニングを説明する公式だからです。ラジオにとって要であるチューニングを避けて通ることはできません。

まず最初に取り組んだのは√の計算。電卓にこの記号があることを思いだし、√の計算の意味をつかもうとしました。1→√→1からはじめて、順に2→√→1.41421356、3→√→1.7320508、4→√→2、5→√→2.2360679、6→√→2.4494897、7→√→2.6457513、8→√→2.8284271、9→√→3、10→√→3.1622776、これをずっと続けていきます。
そのうち、結果が整数になる場合があることに気づきはじめます。そこを突破口に、2→√→1.41421356は1.41421356×1.41421356≒2のことだとわかっていきます。
次にミリ、マイクロ、ナノ、ピコといった単位の計算。はたして、AMラジオの受信に必要なコイルとコンデンサーの数値を公式を用いて算出することができるようになりました。
こうして当時の能力の範囲で取り組んだおかげで「公式を使う」ことができるようになり、√や単位の計算もできるようになりました。訳が分からないからやらないのではなく、訳が分からなくてもなんとかやってみることの重要さを身をもって体験しました。
共振周波数の公式との出会いの最大の収穫は、「なぜ公式にπがあるのか?」という課題を得たことです。最初にその謎が解明されるまでに6年かかりました。高校2年生の時です。ラジオの電波は波、波は三角関数で表されます。そして三角関数は円運動から説明できます。円といえば円周率πです。共振周波数の公式にπが現れる仕組みは三角関数と微分積分によって見事に解明されました。
小学6年生の時から使い始めたのが関数電卓です。これによって決定的に数学の世界に導かれることになりました。sin、cos、tan、log、eといった未知の数学との出会いにわくわくしました。sin30→0.5はなんとか分かりましたが、sin31→0.51503808と出力されることに衝撃を受けました。「どうやって計算しているのだろう?」
トップダウンの学び
「sin31→0.51503808の謎」も高校2年生の時に一つの答えに到達しました。共振周波数の公式と関数電卓「sin31→0.51503808の謎」は私を三角関数と微分積分に導いてくれました。教科書からは決して得られない微分積分のリアリティを手にすることができたのは、自分の中に芽生えた問いに答えようと取り組んだおかげです。
私にとっての「私の数学」は、ラジオ(エレクトロニクス)という現実の中にある数学から始まりました。10歳から6年かけた取り組みは微分積分という壮大な数学物語に結実しました。
高校2年生の時に、微分積分と出会うことができたのは膨大な数の数学書と向き合ったおかげです。学校の図書館の本だけでは物足りず、県立図書館にも出向き微分積分の本を片っ端から手にとってページをめくっていったのです。自分に合った本と出会うまで本と向き合う、今思えばあの時にしかできなかった経験です。
共振周波数の公式と「sin31→0.51503808の謎」にまさか微分積分が関係しているなんて!謎解きの6年間とはすなわち「わからなかった時間」のことです。「私の数学」における「わからない時間」とは、わくわくドキドキの時間です。わからないことがいやだとかネガティブに思ったことはありません。なぜなら人と比べていないからです。
わからないのはわからないからに他なりません。人はまったく関係ありません。自分がわかるまで考えつづけるしか道はありません。このような私が十代で経験したトップダウンの学びを思い起こしてみると、数学に対する絶対的な信用が土台にあったことに気づかされます。
わからないからいやになる、わからないから面白くない、わからないから計算できない、わからないから先に進めない、どれも反対です。わからないことがワクワク、わかならことが面白く、わからなくても計算はできる、わからなくても先に進めるということです。数学があるかないかの心配は不必要で、数学は歴然と存在することに絶対的信用を置いていました。
わからないことが障がいにはならない
わからないことが障がいになると思われているのが「学校の数学」です。自分はわかっているから計算ができると思い込んでいる成績優秀な人でさえ、わかっていることのレベルがどの程度なのかが問題です。時が経てば自分はほとんどわかっていなかったことに気づかされます。
多くの人に知られている三平方の定理ですが、その証明がわからなくても使うことができきます。マイナス同士の積がなぜプラスになるのかを説明ができなくてもマイナスの計算はできます。
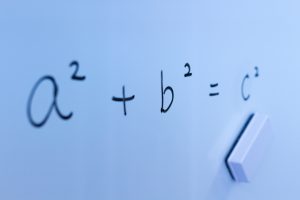
わからないことを理由に数学をしないなんて! わかる・わからないよりも数学をし続けることが重要だということです。数学をし続けることにより、わからないことはいつか本当に理解したいと思うようになります。
わからないことが学びを続けるモチベーションになります。
AI(人工知能)とは数学カタマリマシンのこと
現在であれば、AI(人口知能)、データサイエンスがトップダウンのトップにあたります。AIの正体は機械学習・ディープラーニングと呼ばれる技術です。そこでは微分法が決定的な役割を担っています。
AIの代表例が画像認識です。そこで用いられるのがテンソルとよばれる数学です。ベクトルの上位概念にあたるのがテンソルですが、テンソルによってRGB画像データを表現することができます。また画像認識の出力は確率によって表されます。
AIを支える技術はじめから終わりまで実に多くの数学によって実装されています。まさにAIは数学のかたまりです。AIは数学カタマリマシンと呼んだ方がよほど実体を表します。
プログラミング言語PythonがAI(人口知能)に強い理由はこのような数学の扱いが楽にできる点にあります。
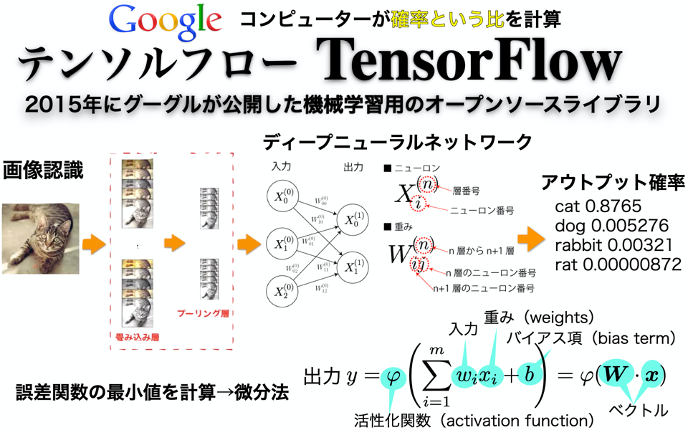
画像認識のPythonコーディングを通してテンソルをはじめとする数学を学ぶことができます。連載第5回で紹介したコサイン類似度では、ベクトルと三角関数を学ぶことができます。
学ぶためのメディアは、本の他にWeb、YouTubeなど多くのメニューがあります。私が40年前に本しかなかった時代とは大きく様変わりしています。トップダウンの学びができる「私の数学」が誰でも実践できる時代になりました。
「学校の数学」に囚われない、自分が自由に選んだ数学──「私の数学」と取り組んでみることで数学という大きな世界の扉を開けることができるのです。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite


