「三角関数よりも金融経済を学ぶべきではないか」
三角関数といえば、高校数学の代名詞ともいえる存在です。役に立たない数学の例としての三角関数が時折話題になります。
「三角関数よりも金融経済を学ぶべきではないか」
という国会議員の委員会での発言(2022年5月17日)がネット上で炎上騒ぎになりました。
サイエンスナビゲーター(R)から言わせると、三角関数がいかに役に立っているかを分からせるのは実は想像以上に難しいのです。ベクトルも微分積分も同じです。
仮に、いかに数学が役に立っているかをわかっている人がそのことを説明したところで、説明された側は「ふう〜ん」で終わるのがオチです。ここに2つの難関があります。
難関その1 いかに数学が役に立っているかを解説する難しさ
難関その2 数学が役に立つことを知っただけでは思った以上に数学への興味関心が大きくならないこと
だから、国会議員を責めてもしかたありません。だって本当に三角関数がどんなに役に立っているかを「実感」していないのですから。はっきりいって、国会議員に「なんとひどいことをいうのか」と責めている人の多くも「ただ知っているだけ」です。この国会議員も知っているようです。「三角関数は我々の生活の基盤を支える人類の英知の1つ」とフォローしつつ上記の発言をしています。その通りです!
そもそも学校で数学がどう役に立っているかを説明できる先生がどれだけいるというのでしょうか。いや先生を社会の大人と言い換えてもいいです。
筆者自身、小中高で一度もきいたことがありません。三角関数どころか中学数学の平方根ですらどう役に立っているのか、いかに役に立っているのか。
難関その1は想像以上に難関です。
難関その2はさらに難関です。
テストのための学校の“数学”の楽しみは点数です。数学それ自体を楽しむことを、テストのための数学から得るのは容易ではありません。
サイエンスナビゲーター(R)はまさに2つの難関に対して取り組み、実践してきました。
三角関数の現場 データサイエンスで使われるコサイン類似度
【ニュースA】メジャーリーグ・エンゼルスの大谷翔平選手がメジャー通算100号ホームランを達成しました。日本の選手では3人目の偉業です。敵地・オークランドでのアスレチックス戦ダブルヘッダーの2試合目、大谷選手は「3番指名打者」で先発出場しました。
【ニュースB】実刑確定の男、刃物持ち逃走また、横浜地検が20日に容疑者の自宅アパートを家宅捜索した際、使用済みとみられる注射器を複数本押収していたことも判明。覚せい剤を使用した可能性もあるとみて鑑定している。
【ニュースC】政府は26日、新型コロナウイルス対策で停止していた海外からの観光客受け入れについて、団体ツアーに限り6月10日から解禁することを決めた。現在5空港にとどまっている国際線の運航については、新千歳空港と那覇空港でも6月中に再開させる。
【ニュースD】岸田総理大臣は現在、停止している海外からの観光客の受け入れを来月10日から再開すると26日、表明しました。海外からの観光目的での入国について「来月10日から添乗員付きパッケージツアー客の受け入れを再開する」と表明しました。
これら4つの文を読むと、内容について、A(スポーツ)とB(事件)は「離れている」、C(社会)とD(社会)は「近い(ほぼ同じ)」とわかると思います。
この判断・判定を人間に代わってマシンに肩代わりさせることができます。コンピューター・プログラムにこれらの文を読み込ませると、次の結果が数値で返ってきます。
AとB:0.126、CとD:0.572
この数値は、大きいほど2つの文は近く、数値が小さいほど2つの文は離れていることを表します。確かに人が読んで判定したのと同じ結果です。
この数値は、2つのデータがどれほど近い(似ている)かを表す指標で「コサイン類似度」と呼ばれるものです。コサイン類似度は高校数学に登場するベクトルと三角関数で説明できます。
データをベクトル化することができれば、ベクトルのなす角を計算することができます。これが内積とよばれる計算です。
データ同士が近い ↔ なす角≒0°
データ同士が離れている ↔ なす角≒180°
と解釈することができます。このとき角度θではなくcosθを指標に使う方が便利です。
データ同士が近い ↔ cos0°≒1
データ同士が離れている ↔ cos180°≒-1
こうして、cosθが1のときピッタリ同じ、-1のとき正反対となります。
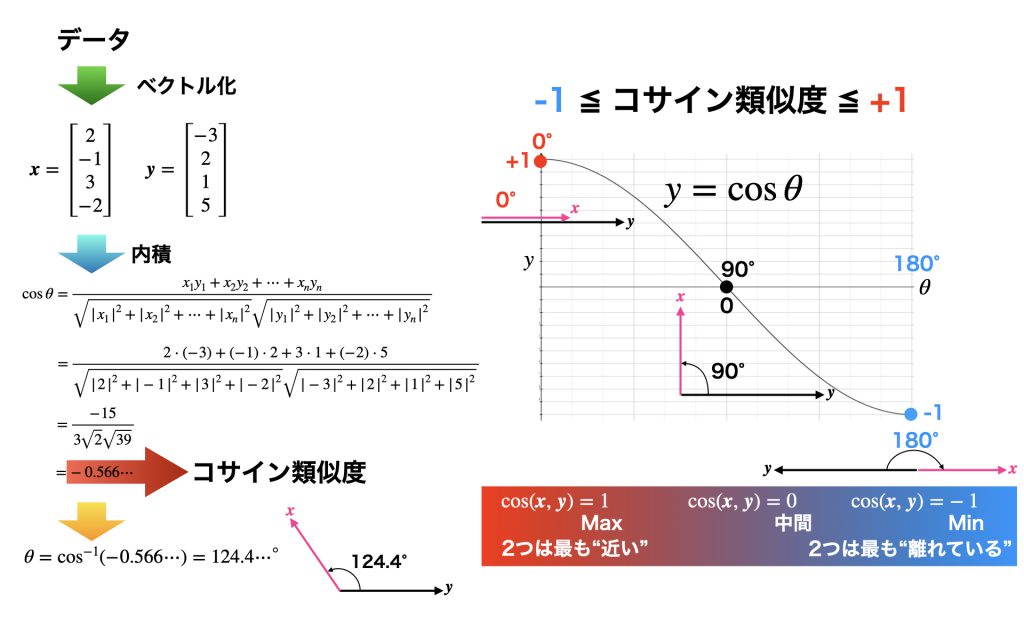
国語が算数にかわるマジック
次が実際のpythonのコードです。

最初に2つの文(ニュースCとD)を定義、次に文書のベクトル化、そしてコサイン類似度を計算する流れです。実行結果が次です。
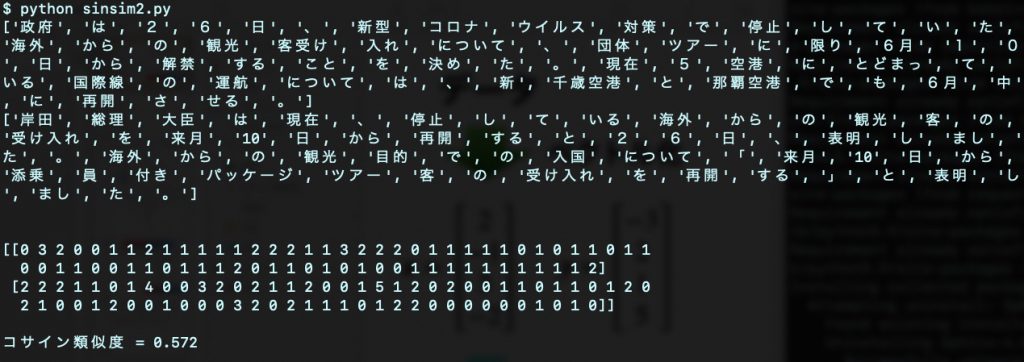
日本語の文章を単語ごとに区切ることで、単語リストをつくります。すると、文に単語が何度出現するのかをカウントします。それがベクトルデータとなります。まさに国語が算数に変わった瞬間です。すると、この2つのベクトルの内積を用いて「コサイン類似度=0.572」が得られます。
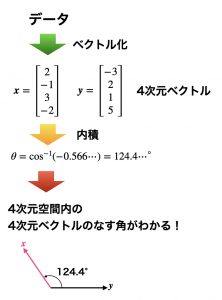
4次元ベクトルのなす角がわかる!
ネット上の膨大なデータをいかに分析するか。コサイン類似度はその一つの技術です。実際にデータサイエンスの現場で使われ役に立っています。これこそ三角関数が役立つ現場です。
ニュースCとDの文をベクトル化すると69単語に分けた69次元ベクトルとなります。コサイン類似度が0.572ということは、2つの69次元ベクトルがなす角度が55.1°ということです。
高校数学では2次元ベクトルと3次元ベクトルまでしかあつかいません。平面と空間内の2つのベクトルのなす角がわかったところであまり驚きはしません。しかし、4次元以上になると話は別です。
私たち人間が見える世界は3次元が限界です。4次元世界を描くことも見ることもできません。しかし、4次元ベクトルは4次元空間に、ニュースCとDをベクトル化したベクトルは69次元世界に実在します。
驚くべきことに数学は、その実在する4次元ベクトル、69次元ベクトルのなす角を見事に計算して私たちにおしえてくれます。これがMathの絶大なる偉力・実力です。
いまだに議論される「数学は何の役に立つのか」
これがMathのリアリティです。学校の“数学”では得ることができないリアリティです。学校の“数学”のすぐそばにMathはあります。今回のベクトルも3次元を1つ次元をあげて4次元にするだけで一気に風景が変わります。
数学ほど役立つものはありません。にもかかわらずいまだに繰り返される「数学は役立つのか」という議論。何度も申しあげているように、本当に数学は難しいことがその最大の原因です。目に見えない数学という存在を自分のものにできていないことを意味します。
Mathのリアリティ。それはMathが自分の外にあるか、中にあるか、ということです。学校の“数学”では、Mathを自分の中にあるようにしていくのは難しいのが現実です。筆者が提案する「私の数学(Math)」では結果として「数学が自分の中にある」ことに気づいていきます。
次回のテーマは「数学の興味・関心力 数学を学び続ける原動力」です。
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite


