ナポレオンの法則の別名、集中効果の法則
ナポレオンの法則はその特徴から様々な呼び方がされます。集中効果の法則もその一つです。トラファルガー海戦からわかるように、軍隊はできるだけ一丸となり一箇所に集中して攻めた方が敵をやっつけるのには効果的だということです。逆に言えば、戦力を2分割、3分割しては弱くなるだけでやってはいけない戦術だということです。
ナポレオンの法則の応用
ナポレオンの法則は私たちに「戦力を集中せよ」とおしえてくれます。例えば、宿題がたくさんある場合、すべてを一気に終わらせようとするとやる気がそがれてしまい手が付けられなくなる経験を誰もがします。
そんな時こそナポレオンの法則(集中効果の法則)を思いだしましょう。国語、数学、英語の宿題があるとき、まずは国語(という敵)だけに集中して戦います。国語を制したならば、次に数学、数学を制したら最後に英語というように1つずつ片付けていく戦術が効果的だということです。
ドイツのフォルクスワーゲン社は他社と競争販売を行う場合に、まず自社独占率が40%を超える値域を1つつくることを最初の目標にする販売戦略を実施しました。エリア全域を一気に相手にするのではなく「戦力を集中せよ」の原則です。
フレデリック・ウィリアム・ランチェスター
以上説明したナポレオンの法則を研究したのがランチェスター(1868-1946)です。イギリスの自動車工学・航空工学のエンジニアです。1916年に「戦争における飛行機-第四の武器のあけぼの」を発表。このレポートの中で、ネルソンやナポレオンの戦法を数学的に分析を行いナポレオンの法則(兵力2乗の法則)を導きました。
最後にその数学を紹介してみましょう。これまでの連載を読んでこられた方ならば理解しやすくなっているでしょう。
時刻tにおけるイギリス軍とフランス軍の人数(隻数)をそれぞれE、Fとします。簡単のため両軍の1人(1隻)同士の強さは同じとします。
すると、戦闘によるイギリス軍人数(隻数)の減少速度(勢い)は敵フランス軍の軍人数(隻数)に比例し、逆にフランス軍人数(隻数)の減少速度(勢い)は敵イギリス軍の軍人数(隻数)に比例すると考えられます。
これを表したのが次の微分方程式です。右辺のマイナスがついているのは減少を表しています。
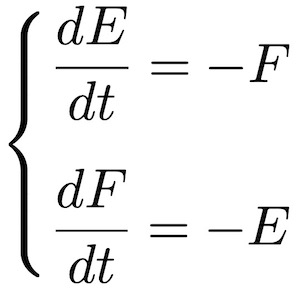
この連立微分方程式を解くと、
Eの2乗−Fの2乗=定数
という結論が得られます。戦力の差が人数(隻数)の2乗の差だということです。
子供は学校の宿題、大人は会社の仕事、私たちは常に片付けなければならないことに囲まれています。それらは戦争の敵ではありませんが、片付けられない時には負けた気持ちにはなります。ナポレオンの法則(集中効果の法則)を思いだして立ち向かってみましょう。そして片付け終わったときに兵力2乗の法則であることを考えてみてください。
女子校生が発端となった1973年豊川信用金庫事件 1973年(昭和48年)12月、愛知県豊川市において突如「豊川信金が倒産する」というデマが広まり、取り付け騒ぎに発展した事件です。14億円の預金が引き出されたことで豊川信金は倒産の危機に陥[…]
執筆者プロフィール

桜井 進(さくらい すすむ)
1968年山形県東根市生まれ。サイエンスナビゲーターⓇ。株式会社sakurAi Science Factory 代表取締役CEO。東京理科大学大学院非常講師。東京工業大学理学部数学科卒。同大学大学院院社会理工学研究科博士課程中退。小学生からお年寄りまで、誰でも楽しめて体験できる数学エンターテイメントは日本全国で反響を呼び、テレビ・新聞・雑誌など多くのメディアに出演。著書に『雪月花の数学』『感動する!数学』『わくわく数の世界の大冒険』『面白くて眠れなくなる数学』など50冊以上。
サイエンスナビゲーターは株式会社sakurAi Science Factoryの登録商標です。
桜井進WebSite
- 1
- 2



