恋の連立微分方程式を解く
微分方程式の右辺にみえる係数a,b,c,dが二人の恋愛傾向・特徴を表します。これが決まれば、次に初期値(恋のはじまり)を決めます。RomeoがJulietのことを一目惚れしし、JulietはRomeoのことが嫌いだったとすると初期値はR(0)=1、J(0)=-1と表されます。これで微分方程式を解くお膳立てが整いました。
現代はコンピューターでこの連立微分方程式+初期値の問題を簡単に解くことができます。そして、その結果をグラフに表すことで時間とともに二人の恋レベルの変化の推移を知ることができます。
さっそく以下に3つのロマンスモデルを見ていきます。注目すべき点は、初期値(恋のはじまり)によって、恋の結末がどうなるかです。

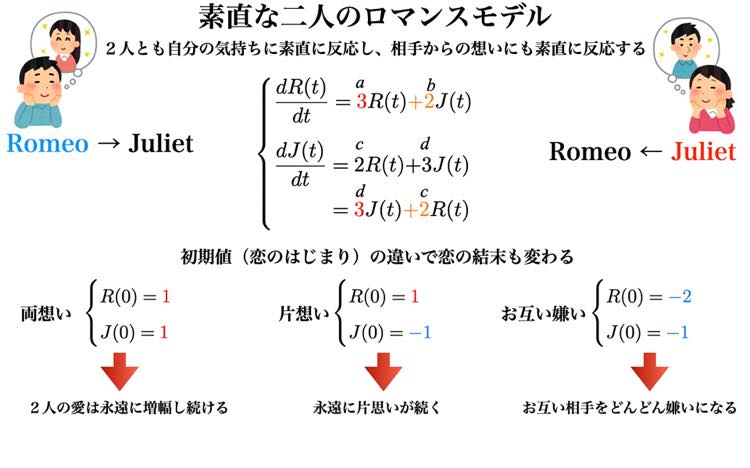
素直な二人のロマンスモデル
2人とも自分の気持ちに素直に反応し、相手からの想いにも素直に反応するとします。自分が相手を好きであればどんどん好きになり、相手が自分を好きだと知れば相手をどんどん好きになるという場合です。
初期値が両想い、片想い、お互い嫌いの3ケースを考えてみます。これは方程式を解くまでもなく予想がつきます。コンピューター・シミュレーションの結果は、両想いであればどんどん好きになっていく、つまり結末は二人の恋レベルが爆発するということです。片想いとお互い嫌いはそれぞれ片想いが爆発し、お互いをどんどん嫌いになるということです。
瓜二つの二人のロマンスモデル
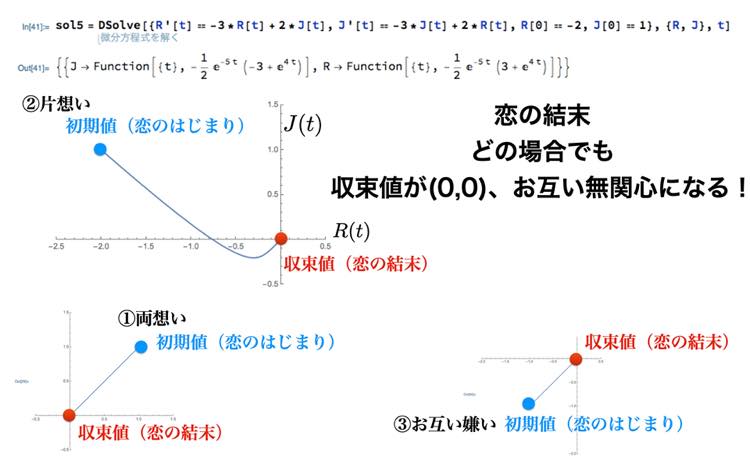
2人とも、相手への想いは素直でない(好きなるほど覚めていく)が、相手からの想いには素直に反応するモデルです。前半が係数aとcが負、後半が係数bとdが正を表します。瓜二つなのでそれらの値も同じとします。
初期値は前のモデルと同じ3つの場合を考えます。コンピューター・シミュレーションの結果はどの場合も、収束値が原点(0,0)となります。R(t)とJ(t)が0ということなのでお互い無関心というのが恋の結末です。

▶︎次のページ「不運なロマンスモデル」
次のページへ



