コンピューター・シミュレーション
マルサスのモデルをコンピューター・シミュレーションしてみましょう。
AI(人工知能)のプログラミング言語としても用いられているPythonを使って微分方程式①を解いてみます。
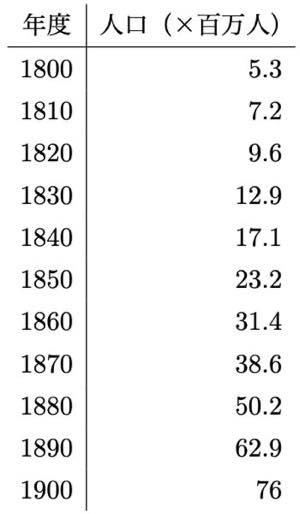
実際の人口統計を用いてマルサス・モデルの検証を行ってみます。次の表は米国の1800年から1900年までの人口です。
微分方程式①を解くには、比例定数kと人口の初期値N(0)を与える必要があります。最初の1790年を時刻t=0として、人口の初期値N(0)は530万人です。
1800年と1810年の2つのデータから比例定数をk=0.306と決めることができます。
これでマルサス・モデルのコンピューター・シミュレーションを行う準備完了です。
次がその結果です。
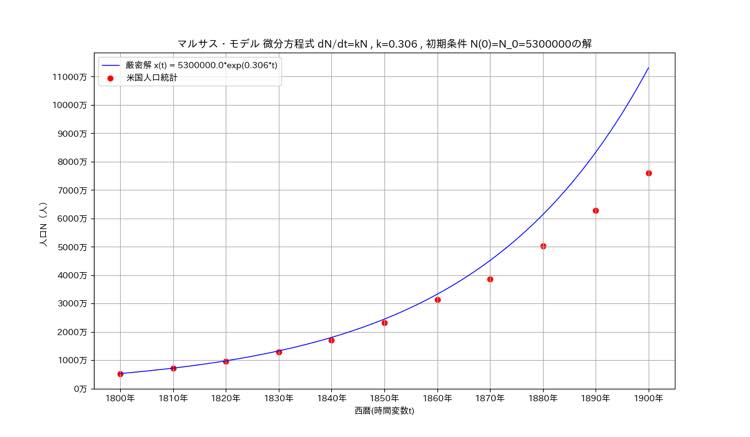
実際の人口統計との比較は、1800年から1860年まではかなりの一致が見られます。それ以降は誤差が次第に大きくなっていきます。
グラフから分かるように人口は直線的に増加するのではなく増加の度合いが大きくなる曲線を描くことが分かります。これが指数曲線といい、人口は指数関数的に増加するなどと呼ばれます。このことをマルサスは次のように表現しました。
人口は制限されなければ幾何級数的に増加するが生活資源は算術級数的にしか増加しないので、生活資源は必ず不足する。
ここでいう「幾何級数」が指数関数(指数曲線)を意味し、「算術級数」が1次関数(直線)を意味します。
人口推移がこの最も単純なモデルで説明できる時代は確かにあります。しかし、現代は人口増減の原因・要素が複雑になりこのモデルでは到底説明できません。そもそも指数関数的増加が続けば人口爆発を招くわけですがそうはなっていません。現在までに現実の人口推移を説明するモデルは数多く出されています。その出発点がこのマルサス・モデルです。
▶︎次のページは「Pythonプログラミング」
次のページへ


