フェヒナーの法則
エルンスト・ウェーバーの弟子であるドイツの物理学者・心理学者グスタフ・フェヒナー(1801-1887)は、ウェバーの法則を発展させました。
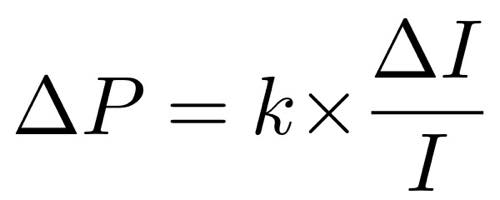
ここで、定量的な考察を行うために、感じ方を感覚量P(感覚Perception)、重さを刺激の強度I(Intensity of stimulation)とします。
重さの増分10gの感じ方は始めの重さが100gか1000gで異なります。正確には、増分に対する感じ方の増分は、始めの重さに反比例すると考えることができます。100gの場合の増分10gに対する感じ方の増分は、1000gの場合のそれよりも10分の1だということです。
すなわち、感覚量Pの増分ΔPは、刺激の強度Iに反比例するということ。そして、そもそも感覚量Pの増分ΔPは、刺激の強度の増分ΔIに比例すると考えられます。重さの例でいうならば、始めの重さを100gとした場合、重さの増分ΔIが10gから2倍の20gになると、感覚量Pの増分ΔPも2倍になるということです。
したがって、感覚量Pの増分ΔPは、刺激の強度Iに反比例し、刺激の強度の増分ΔIに比例するということになるので、比例定数をkとおくと次のように表すことができます。
すると、増分ΔP、ΔIをそれぞれdP、dIと置いた関係式が微分方程式と呼ばれるものです。

微分とは“勢い”のことです。例えば、車の速度は位置の微分(勢い)のことで、加速度は速度の微分(勢い)のことです。一定の速度60km/hで走っている場合、速度の勢い(微分)、すなわち加速度は0です。アクセルを踏めば、時速が70 km/h、80 km/hと大きくなります。このときが加速度が正です。ブレーキを踏めば時速は60 km/h、30 km/h、0km/h(停止)と変化します。これときが加速度が負です。
微分方程式とは、刻々と変化する“微分”が何によって決まるかを表した式のことです。
積分することでPとIの関係を導出することができます。

これがフェヒナーが導き出した結論(1860年に出版)です。現在ではウェバー・フェヒナーの法則と呼ばれています。
数式のポイントは対数log。ざっくり説明すれば、「対数とはかけ算の回数」です。たとえば、1000=10×10×10。1000は10を3回かけ算した数なので、1000の対数は3となります。
▶︎次のページは「フェヒナーの法則」
次のページへ


